493. Компланарны ли векторы: а) а{—1; 2; 3}, i + j и i — k; б) b{2; 1; 1,5}, i + j + k и i —j; в) а{1; 1; 1}, b(1; —1; 2} и с (2; 3; -1}?

Для решения задачи установим, можно ли вектор a разложить по векторам b и c , т.е. существуют ли m и n, удовлетворяющие условию

а)

Запишем равенство

в координатах:

Равенства (x), (2) и (3) выполняются при m=2, n=-3, т.е., векторы а , b и c компланарны.

б)

Запишем равенство

в координатах:

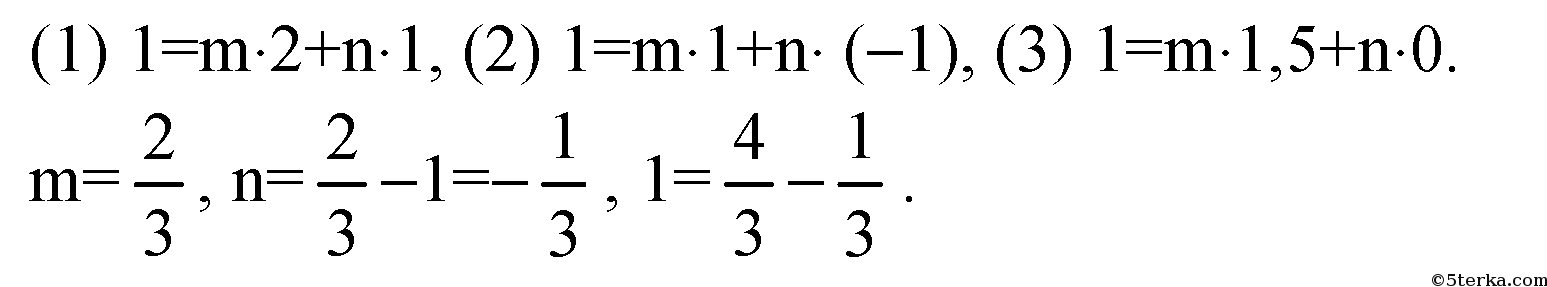
Равенства (1), (2) и (3) выполняются при

т.е., векторы a,

b и c компланарны. в) Запишем равенство

в координатах.

Система уравнений не имеет решений. Т.е. векторы a,

b и c не компланарны.