Введем прямоугольную систему координат Oxyz. Тогда С (0; 3; 0), В (4; 0; 0).
Точка N — середина отрезка СВ;

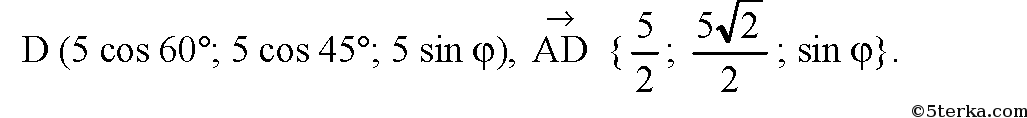

следовательно,

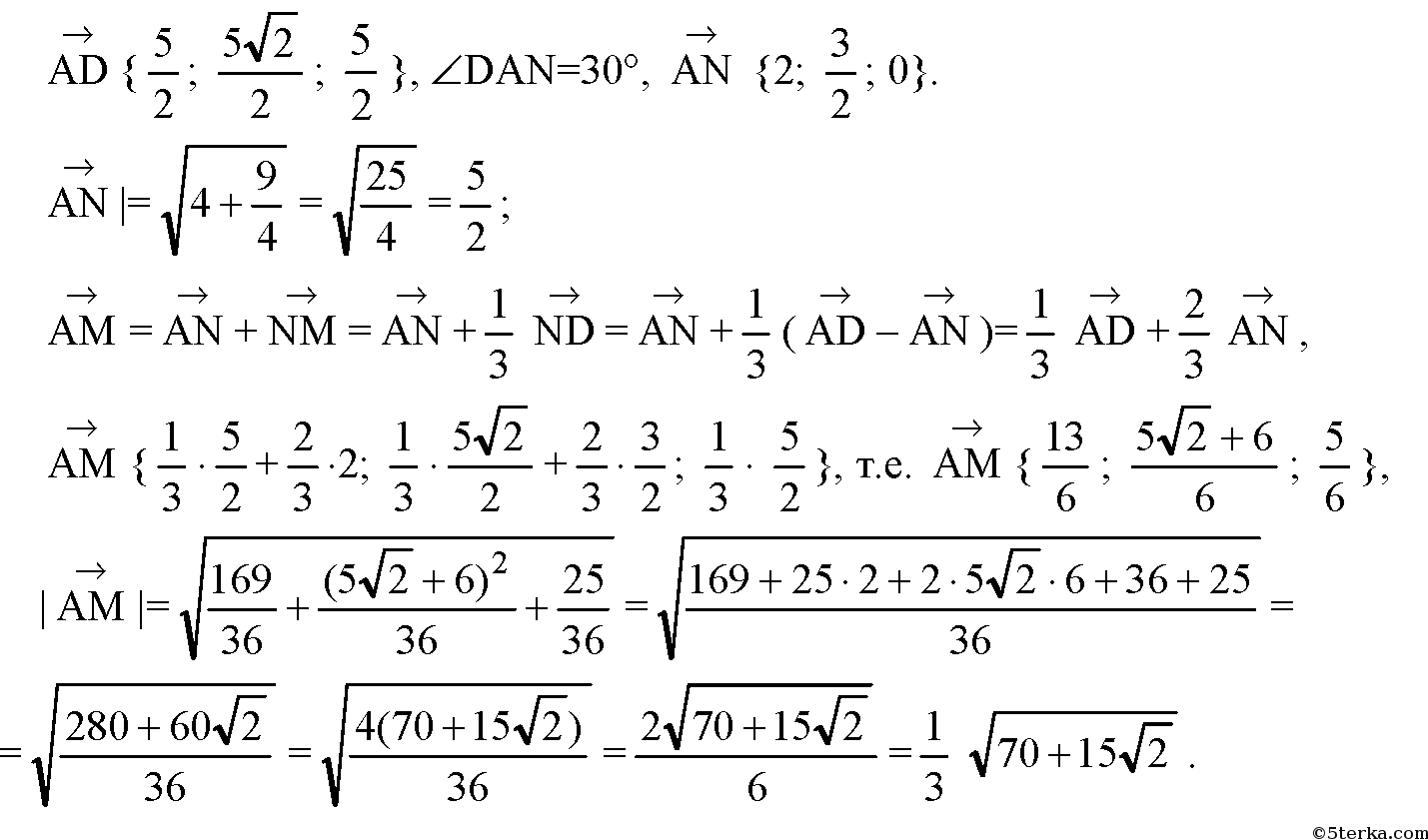
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №475
к главе «Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов».
Комментарии