440. Отрезок CD длины т перпендикулярен к плоскости прямоугольного треугольника ABC с катетами АС = b и ВС = a. Введите подходящую систему координат и с помощью формулы расстояния между двумя точками найдите расстояние от точки D до середины гипотенузы этого треугольника.
Введем прямоугольную систему координат с началом в точке С и с осями: Ох — по отрезку СА, Оу — по отрезку СВ, тогда точка D будет лежать на оси Оz. Пусть точка К — середина АВ. Во введенной системе координат A (b; 0; 0), B (0; а; 0), С (0; 0; 0), D (0; 0; m).
Точка
Подставляя координаты точек А и В, получим:
Следовательно:
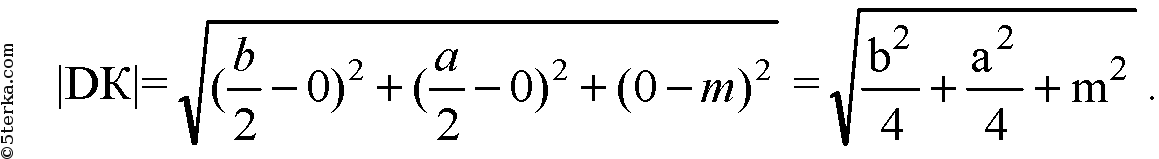
Источник:
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №440
к главе «Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора.».
Комментарии