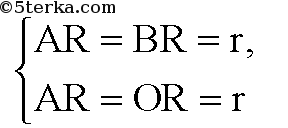
где r — радиус окружности;
Точки А, О, В и R лежат в одной плоскости.
Точка О (0; 0; 0) совпадает с началом координат, А (4; 0; 0) лежит на оси
Ох; В (0; 6; 0) лежит на оси Оу, следовательно, ΔAOB лежит в координатной плоскости Оху, тогда, центр описанной окружности лежит в той же плоскости. Следовательно, координаты центра: R (х; у; 0). По формуле расстояния между двумя точками:
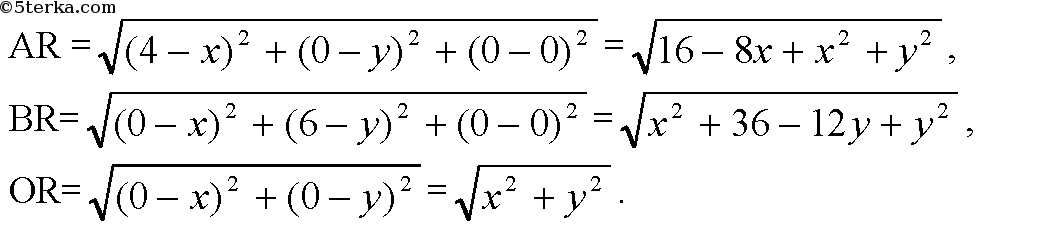
Можем записать систему уравнений:
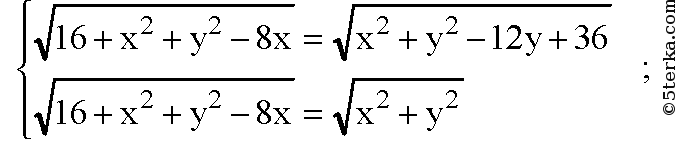
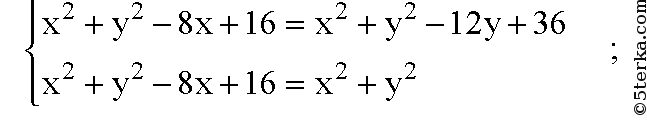
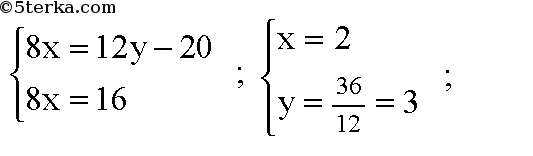
Координаты центра окружности, описанной около ΔAOB: R (2; 3; 0). Радиус описанной окружности равен AR=BR=OR=r,
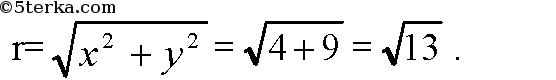
б) Если точка R (х; у; z) равноудалена от вершин тетраэдра ОАВС, то
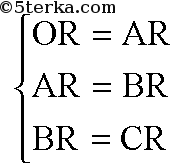
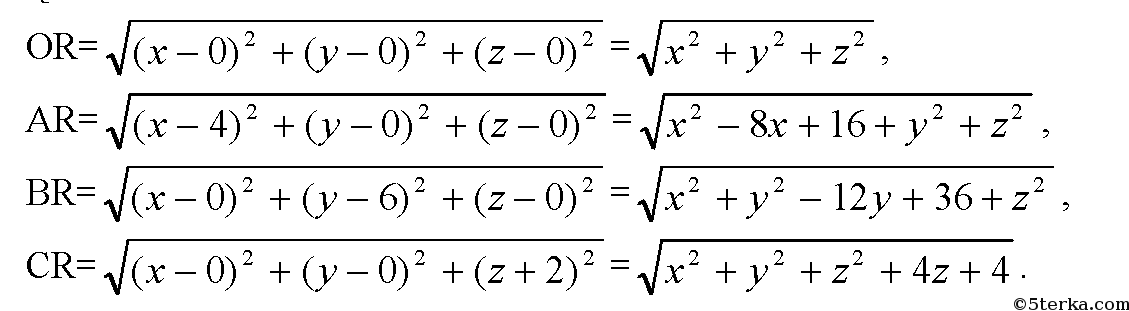
Можем записать систему уравнений:
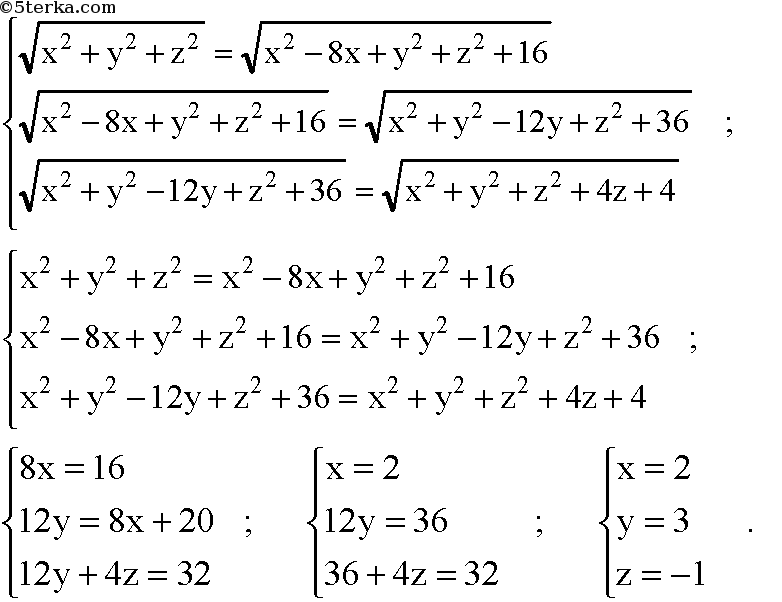
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №439
к главе «Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора.».