431. Определите вид треугольника ABC, если: а) A (9; 3; —5), В (2; 10; -5), С (2; 3; 2); б) A (3; 7; -4), В (5; -3; 2), С (1; 3; — 10); в) A (5; -5; -1),В(5; -3; -1), С (4; -3;0); г) A (-5; 2; 0), В ( — 4; 3; 0), С (-5; 2; -2).

Сравним длины сторон треугольника. Для этого по формуле расстояния между двумя точками

найдем

Если a=b=c, то треугольник ABC — равносторонний. Если:

с=b ≠ a, то треугольник равнобедренный, если нет одинаковых сторон: с ≠ b ≠ а, то есть если а > b ≥ с, то следует проверить, выполняется ли теорема Пифагора. Если да, то ΔABC — прямоугольный.

а)

AB=ВС=АС, треугольник равносторонний.

б)

Проверим, выполняется ли равенство:

— верно. Следовательно, треугольник ABC — прямоугольный.

в)

Проверим, выполняется ли равенство

6=4+2 — выполняется. Следовательно, треугольник ABC — прямоугольный равносторонний.

г)

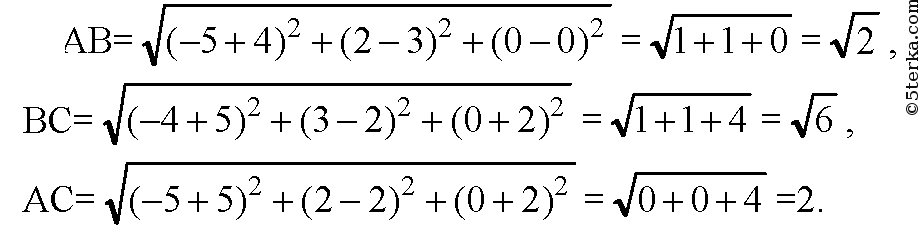
Проверим:

Следовательно, треугольник ABC —

прямоугольный равносторонний.