398. Треугольники ABC, A1B1C1 и A2B2C2 расположены так, что точки А, В, С являются серединами отрезков А1А2, В1В2, С1С2 соответственно. Докажите, что точки пересечения медиан треугольников ABC, А1В1С1 и A2B2C2 лежат на одной прямой.

398. Треугольники ABC, A₁B₁C₁ и A₂B₂C₂ расположены так, что точки А, В, С являются серединами отрезков А₁А₂, В₁В₂, С₁С₂ соответственно. Докажите, что точки пересечения медиан треугольников ABC, А₁В₁С₁ и A₂B₂C₂ лежат на одной прямой.

O, O₁, O₂ — точки пересечения медиан (рис. 238). Тогда

Поэтому

Но О — центр тре угольника А₁В₁С₁, поэтому

Таким образом.

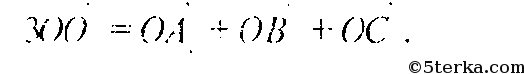
Аналогично

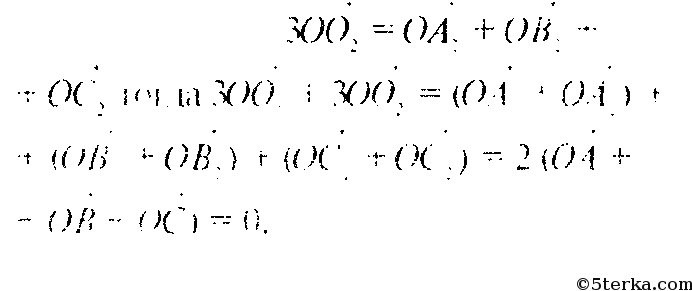
Но это означает, что векторы OO₁ и OO₂ — коллинеарны, а значит прямые OO₁ и OO₂ параллельны. Так как есть общая точка, то эти прямые совпадают. Значит точки О, О₁, О₂ лежат на одной прямой.

Источник:

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №398
к главе «Глава IV. Векторы в пространстве Дополнительные задачи».

Все задачи

← 397. В тетраэдре ABCD точки М и N являются соответственно точками пересечения медиан граней ADB и BDC. Докажите, что MN||AC, и найдите отношение длин этих отрезков.

399. Докажите, что треугольник, вершинами которого являются точки пересечения медиан боковых граней тетраэдра, подобен основанию тетраэдра. →

Комментарии