203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярная к плоскости треугольника. Найдите расстояние от точки К до сторон треугольника, если АВ=ВС=10 см, АС =12 см, ОК = 4 см.

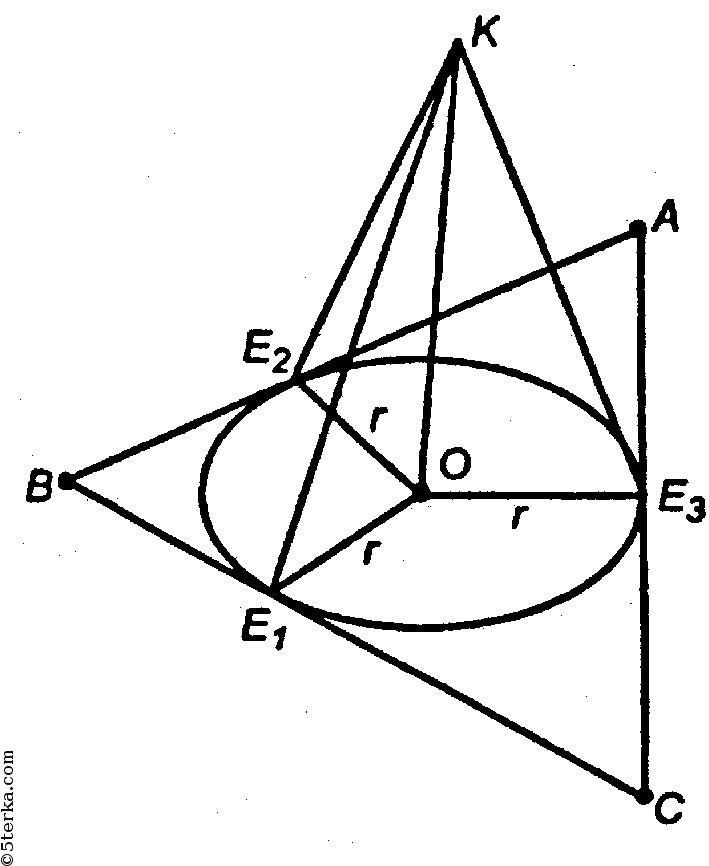
Дано:

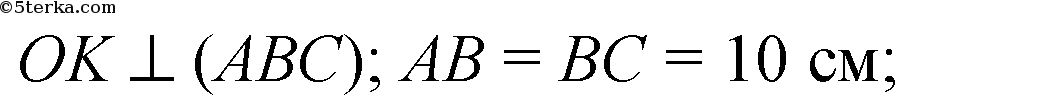
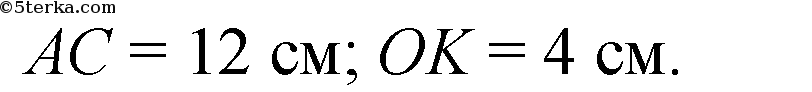
Решение:

В точки касания сторон ΔАВС с окружностью проводим отрезки ОЕ₁, ОЕ₂ и ОЕ₃.

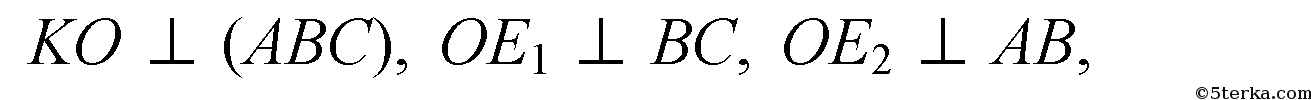
то по теореме о 3-х перпен

дикулярах,

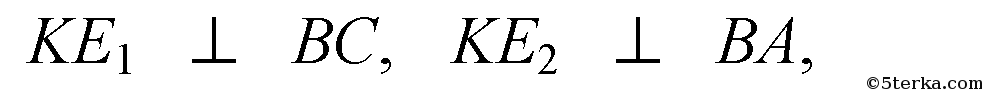
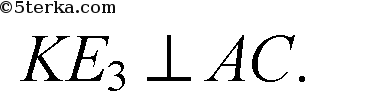
Т.о. KE₁, E₂K и KE₃ суть искомые

расстояния. Поскольку проекции этих отрезков на плоскость ΔАВС равны (они равны r - радиусу вписанной окружности), то и отрезки равны:

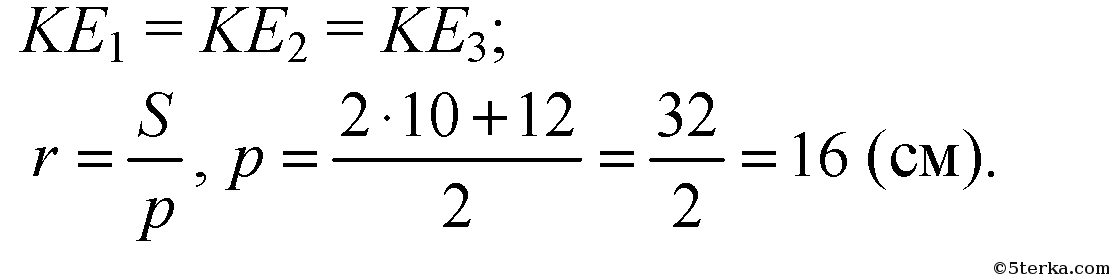
Применим формулу Герона:

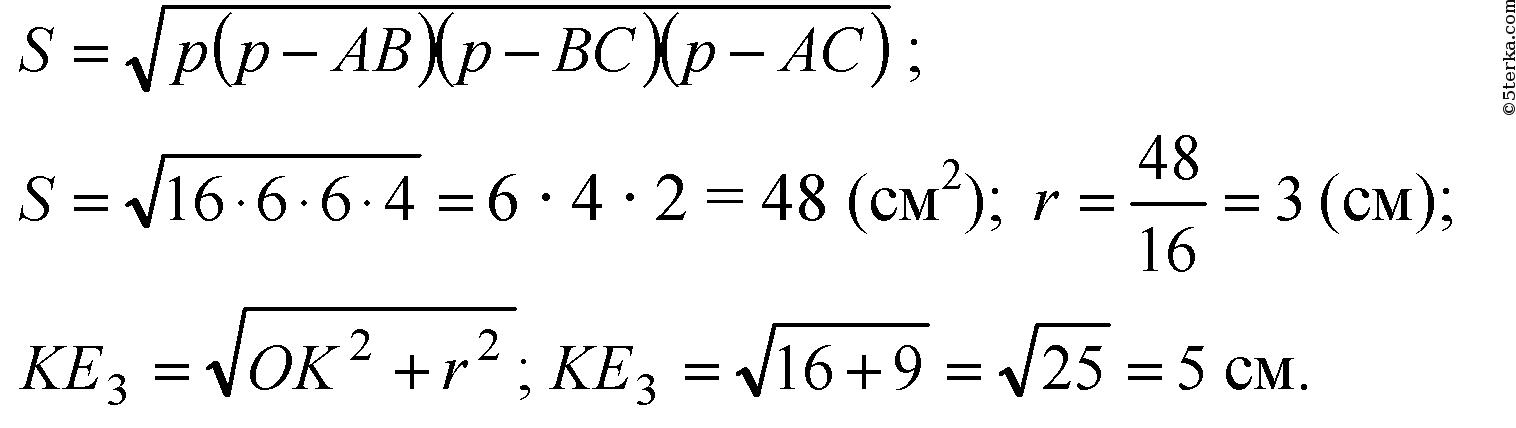
Ответ: 5 см.