* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Дано: ABCD - тетраэдр;
Определим линейную меру двугранного угла DACB.
ADC ⊥ пл. АВС, тогда двугранный угол DACB и соответствующий ему линейный угол DCB равны 90о.
Определим линейную меру двугранного угла DABC.
Проведем отрезок СМ ⊥ АВ, соединим точки М и D.
то по теореме о 3-х перпендикулярах,
По определению, ∠DMC - линейный угол двугранного угла DABC.
По теореме Пифагора:
Тогда
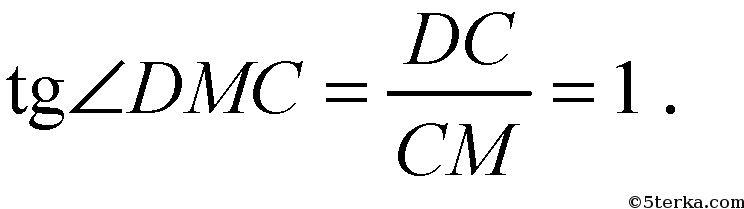
Отсюда
Определим линейную меру двугранного угла BDCA.
то ∠АВС - линейный угол двугранного угла
Ответ:
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №173
к главе «Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей.».