159. Прямая ВМ перпендикулярна к плоскости прямоугольника ABCD. Докажите, что прямая, по которой пересекаются плоскости ADM и ВСМ, перпендикулярна к плоскости АВМ.

Дано:

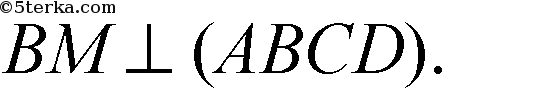
Решение:

МЕ - линия пересечения плоскостей AMD и ВСМ. В плоскости AMD проводим DE || AM. AM ⊥ AD - по теореме о 3-х перпендикулярах, то DE ⊥ AD.

AD ⊥ MB, AD ⊥ AB, то по теореме о 3-х перпендикулярах AD ⊥ пл. АМВ. Отсюда следует, что МЕ ⊥ пл. АМВ (т.к. ME || AD). Что и требовалось доказать.