142. Концы отрезка отстоят от плоскости α на расстояниях 1 см и 4 см. Найдите расстояние от середины отрезка до плоскости α.

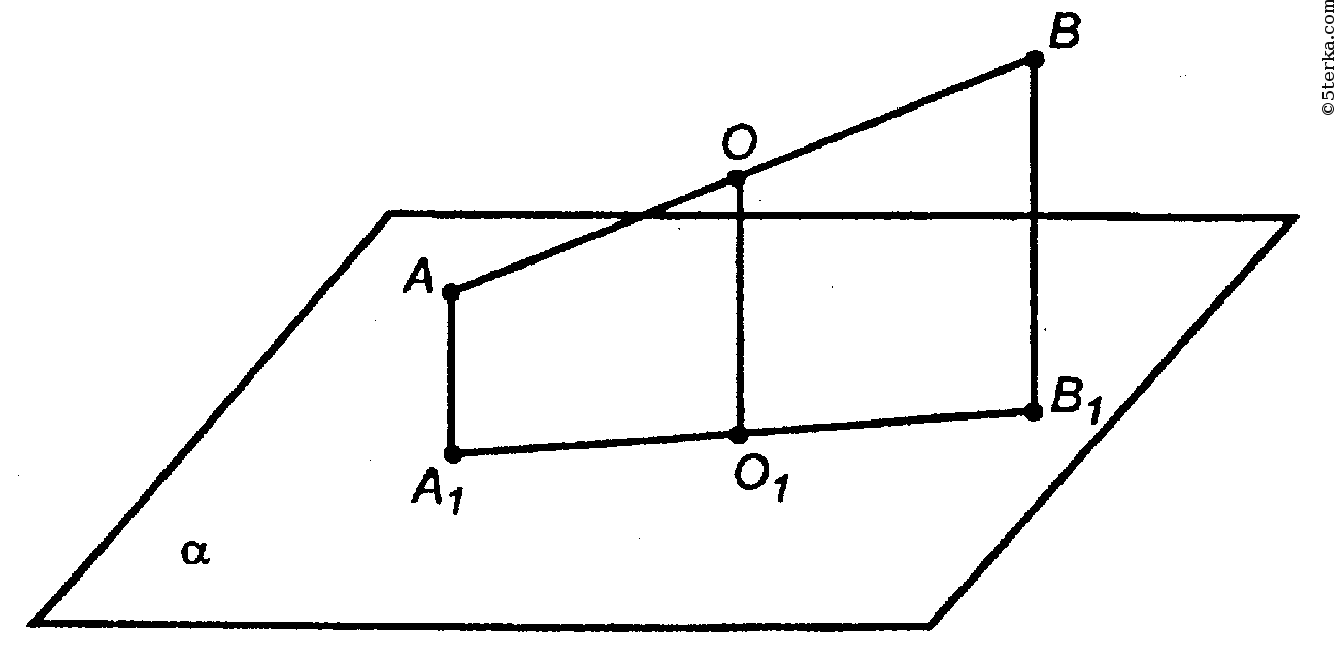
Дано:

Рассмотрим два случая:

Случай I. Если АВ не пересекает α, то имеем: АА₁ = 1 см, ВВ₁ = 4 см, О - середина АВ;

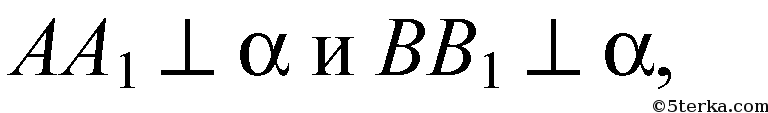
то

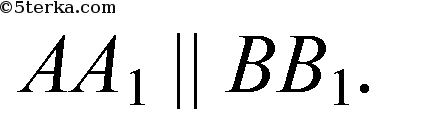
Согласно аксиоме, через АА₁ и ВВ₁ можно провести единственную плоскость АВВ₁А₁.

В пл. АВВ₁А₁ проводим ОО₁ || ВВ₁. Согласно п. 21^о, т. О ∈ А₁В₁. Значит, ОО₁ ⊥ α, ОО₁ - искомый отрезок. р(О, α) = ОО₁.

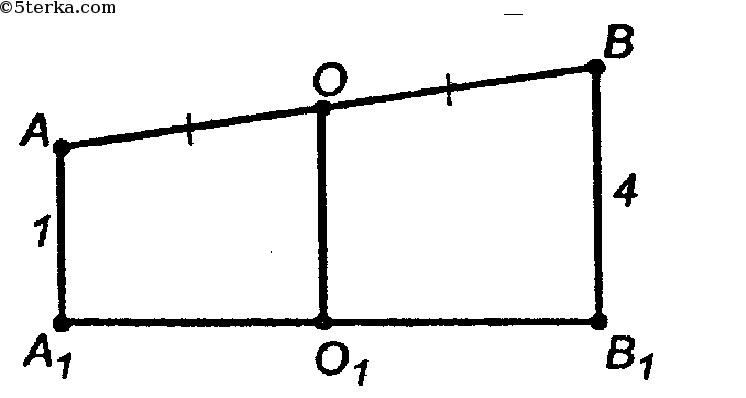
Т.о. ОО₁ - средняя линия трапеции;

Случай II. АВ пересекает пл. а

Продолжим О₁О до пересечения с А₁В и АВ₁ в точках Е и F.

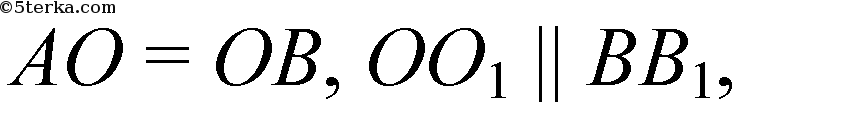
то по теореме Фалеса

по теореме Фалеса

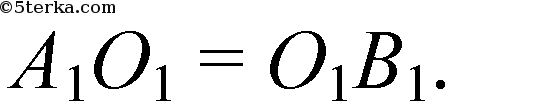
В ΔАА₁В₁: О₁F - средняя линия, то есть

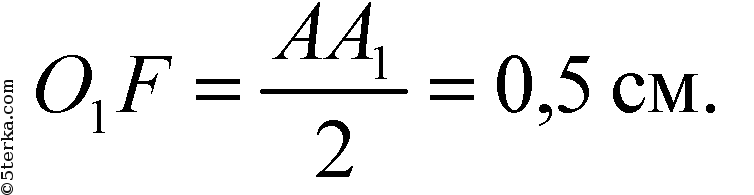
- средняя линия, то есть

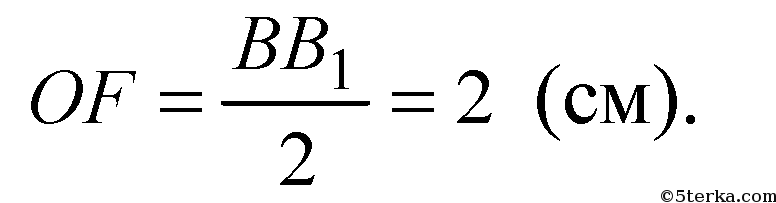
Ответ: 2,5 см или 1,5 см (в зависимости от того, пересекает ли АВ плоскость а).