137. Докажите, что через каждую из двух взаимно перпендикулярных скрещивающихся прямых проходит плоскость, перпендикулярная к другой прямой.

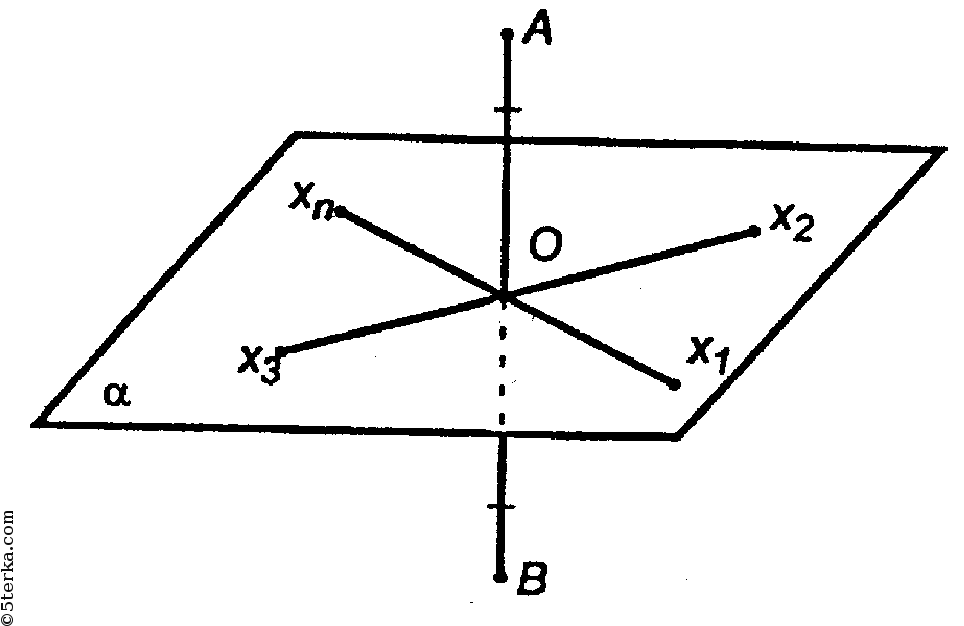
Решение

Пусть скрещивающиеся прямые а и b лежат в параллельных плоскостях (известная теорема).

1. Проведем через b пл. β; β || a.

2. Проведем АА₁⊥β и ВВ₁⊥β.

3. По теореме

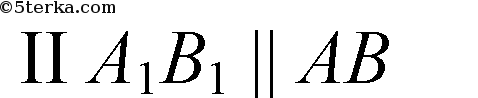
(если

то

4.

5. Из т. С₁ проведем С₁С ⊥ β. Она пересечет АВ в точке С (b ⊥ пл. АС₁А₁. В пл. АС₁А₁ проведем С₁С || A₁A. Тогда b ⊥ С₁С - по определению. Если найдется прямая С₁С₂ ⊥ β и С₂ не совпадает с С, тогда через т. С₁ будет проходить 2 плоскости, перпендикулярные к b: пл. А₁АВВ₁ и пл. СС₁С₂; а это невозможно).

Итак,

6.

Т.о. через а проходит плоскость ⊥ к b. Что и требовалось доказать.