134. Докажите, что все прямые, проходящие через данную точку М прямой а и перпендикулярные к этой прямой, лежат в плоскости, проходящей через точку М и перпендикулярной к прямой а.

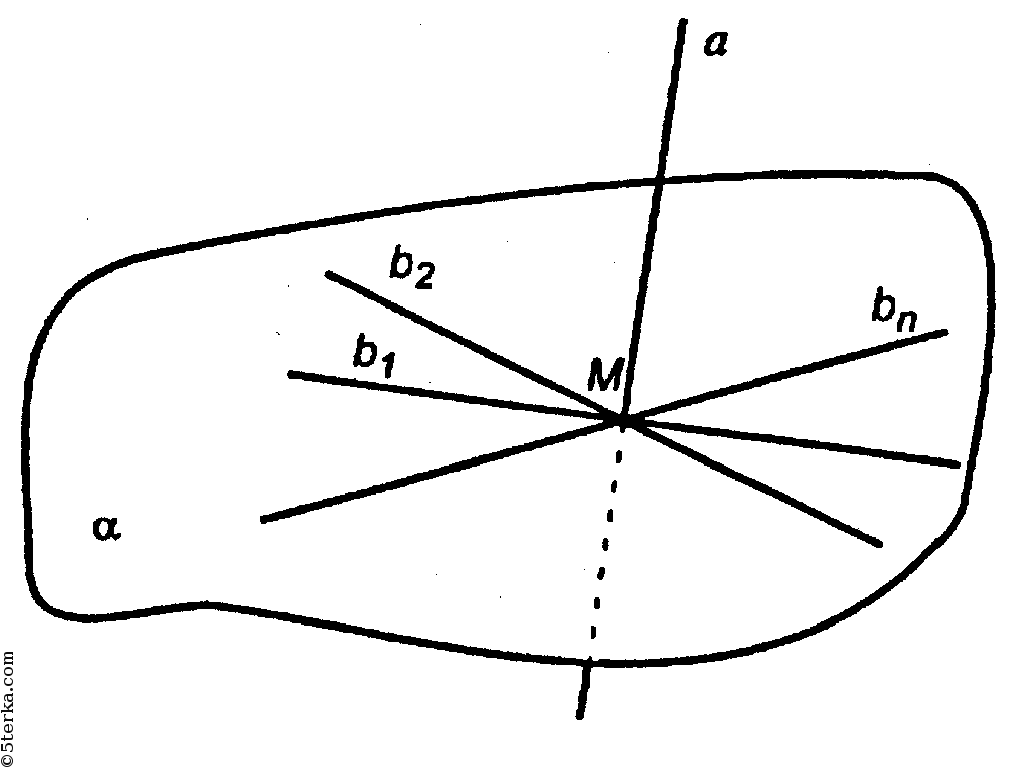
Дано:

Решение:

т.е. b₁ и b₂ пересекаются.

Из вышеперечисленных фактов следует, что по признаку перпендикулярности прямой и плоскости прямая а перпендикулярна α. Через две пересекающиеся прямые можно провести плоскость, и притом единственную, следовательно, любая прямая b_n, проходящая через т. М и перпендикулярная к а, лежит в α.

Предположим b_n ⊄ α.

То через b₂ и b_n можно провести плоскость γ и:

Следовательно, через т. М проходит сразу две плоскости α и γ ⊥ а, а через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой. Значит, наше предположение неверно и b_n ⊂ а.

Что и требовалось доказать.