119. Прямая ОА перпендикулярна к плоскости ОВС, и точка О является серединой отрезка AD. Докажите, что: a) AB = DB; б) AB=AC, если ОВ=ОС; в) OB = OC, если АВ=АС.

Решение:

а) Рассмотрим ΔABD.

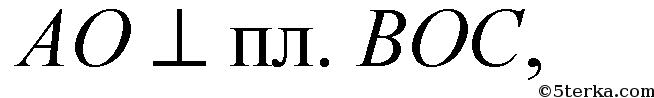
поэтому

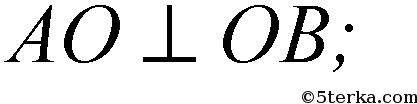
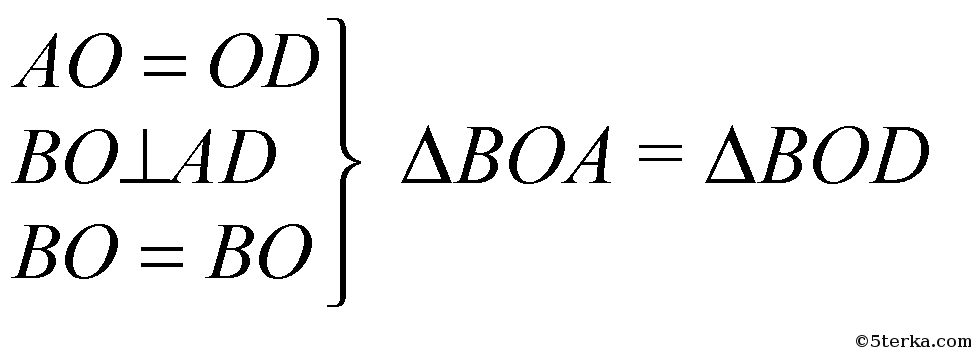
- по двум катетам,

б) Рассмотрим ΔАОВ и ΔАОС.

- по определению;

- по условию;

- общая.

Треугольники АОВ и АОС равны по двум катетам. Отсюда:

в) Т.к. АВ = АС, то прямоугольные треугольники АОВ и АОС равны по гипотенузе и катету (АО - общий катет), поэтому

Что и требовалось доказать.