15. Три прямые попарно пересекаются. Докажите, что они либо лежат в одной плоскости, либо имеют общую точку.

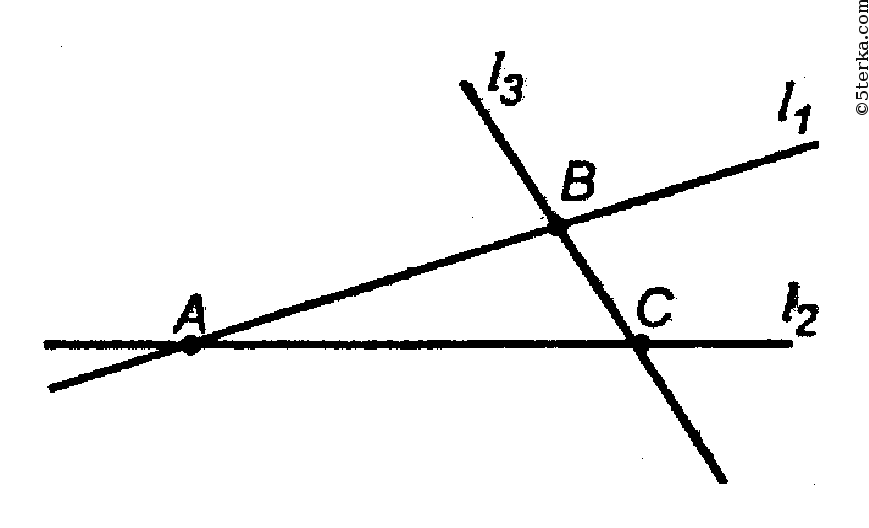
Каждая из трех точек принадлежит одновременно прямым.

Через три точки по аксиоме А₁ можно провести единственную плоскость α. Поэтому отрезки АВ,

ВС и АС лежат в плоскость α

(по аксиоме А₂), значит, прямые, которым принадлежат эти отрезки, тоже лежат в α.

Рассмотрим второй случай:

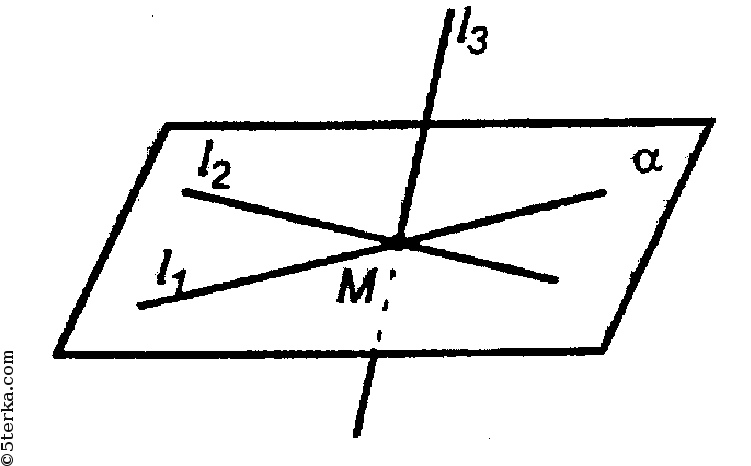
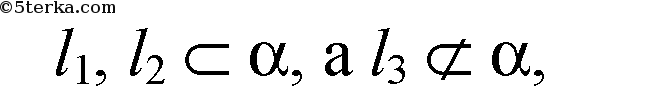
но и пересекается с l₂ и l₁ в точке М.

То есть прямые имеют общую точку, но не лежат в одной плоскости.