Рассмотрим осевое сечение шара.
Тогда
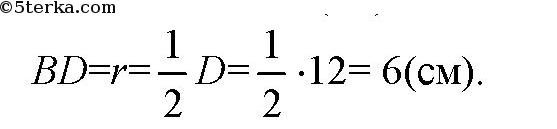
Так что в ΔDBO по теореме Пифагора получим:
Площадь искомой поверхности равна сумме площади боковой поверхности цилиндра с радиусом основания, равным DB, и высотой BM=2⋅OD =2⋅8=16(см) и площади S'', равной разности площадей шара и двух шаровых сегментов с высотой
То есть
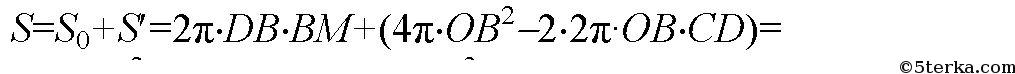
Источник:
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №37
к главе «§ 23. Объемы и поверхности тел вращения».
Комментарии