47. Решите предыдущую задачу в случае правильной усеченной треугольной пирамиды.

Дополним данную усеченную пирамиду до полной. Проведем высоту O2O. Так как в правильной пирамиде высота проходит через центр окружности, вписанной в основание, то MO и М₁О₁ — радиусы окружностей, вписанных в ΔABC и ΔA₁B₁C₁. Далее площади

равны ΔABC и ΔA₁B₁C₁ равны

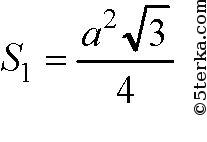
и

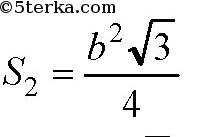
соответстсоответственно, а радиусы вписанных окружностей

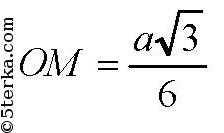
и

Поскольку ОМ⊥АВ, то ∠M₁MO=α — линейный угол данного дву гранного угла. В прямоугольной трапеции ММ₁О₁О проведем M₁K⊥MO, тогда

Далее в ΔM₁MK:

Так что

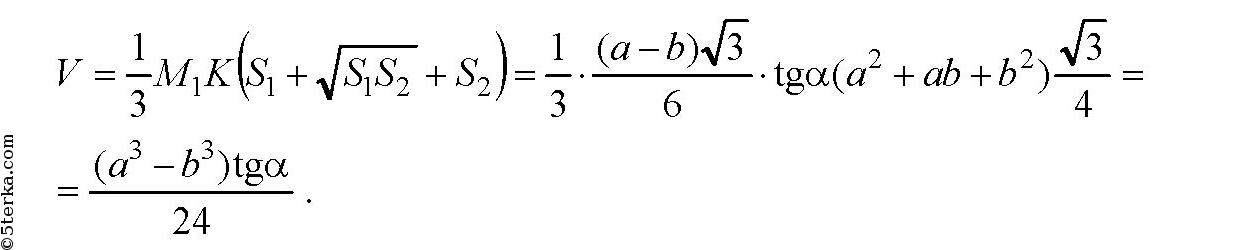
Источник:

Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №47
к главе «§22. Объемы многогранников».

Все задачи

← 46. В правильной усеченной четырехугольной пирамиде стороны нижнего и верхнего оснований равны а и b, а двугранный угол при ребре нижнего основания равен а. Найдите объем пирамиды.

48. Через середину высоты пирамиды проведена плоскость, параллельная основанию. В каком отношении она делит объем пирамиды? →

Комментарии