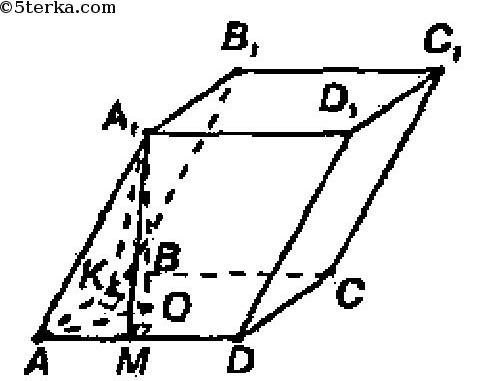
Проведем перпендикуляр А1О к плоскости основания, а также A1M⊥AD и A1K⊥AB. Тогда по теореме о трех перпендикулярах OM⊥AD и ОК⊥АВ. ΔAA1М=ΔAA1K (по гипотенузе и острому углу 2а). Так что AK=AM=AA1⋅cos2a=cos2a. Далее, ΔAМО=ΔAКО (по гипотенузе и катету). Так что ∠КAО=∠МAО=α.

Далее, в прямоугольном ΔAA1О по теореме Пифагора получаем:
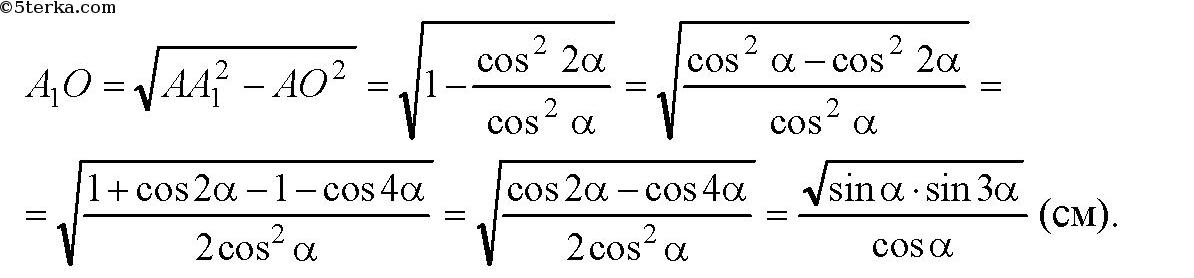
Далее, основание параллелепипеда — ромб с площадью S=AВ⋅AD⋅sinα=1 ⋅ 1sin2α=sin2α (см2). Тогда объем

Источник:
 Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №17
к главе «§22. Объемы многогранников».
Комментарии