43. Шар радиуса R вписан в усеченный конус. Угол наклона образующей l к плоскости нижнего основания конуса равен α. Найдите радиусы оснований и образующую усеченного конуса.

Рассмотрим осевое сечение, которое является трапецией ABCD, причем АВ=CD. ∠BAD=α. Проведем BM⊥AD. Тогда BM=O₁O₂=2R.

В ΔАВМ:

Центр вписанной в ABCD окружности лежит на пересечении биссектрис, так что АО и ВО — биссектрисы, то есть

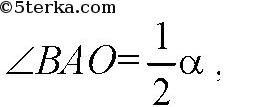
Так что ΔАВО — прямоугольный, поэтому

Далее, в прямоугольном ΔBОО₁:

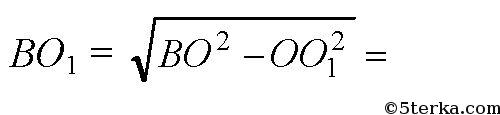
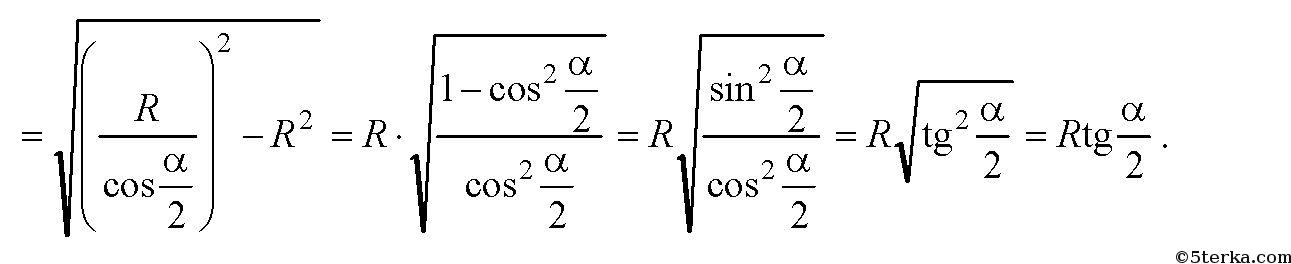
Так как отрезки касательных, проведенных из одной точки к окружности, равны, то BК=BО₁ и AO₂=AK.

Тогда

Ответ:

Источник:

Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
задача №43
к главе «§21.Тела вращения».

Комментарии