Угол между радиусами, проведенными в эти точки, равен 60°. Найдите угол X между проведенной прямой и осью цилиндра.

Через данные точки А и С проведем плоскость ABCD, параллельную оси. Соединим точки В и О1. Угол между радиусами, проведенными в данные точки А и С соответственно из О и O1 будет равен углу ∠BO1C = 60°.
Следовательно, равнобедренный ΔBO1С является равносторонним и BС = 0,5 = К. Искомый угол X между проведенной прямой А С и осью цилиндра равен ∠BAC. В прямоугольнике ABCD AB=D=2R (по условию). Тогда из прямоугольного ΔABC

Ответ:
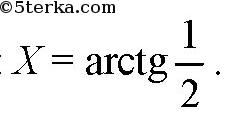
Источник:
 Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №6
к главе «§21.Тела вращения».
Комментарии