78. Найдите полную поверхность правильной усеченной пирамиды: 1) треугольной; 2) четырехугольной; 3) шестиугольной, если высота h, а стороны оснований а и b.

Проведем ОК ⊥ АВ и ОК₁ ⊥ А₁B₁.

Высота OO₁ = h проходит через центры окружностей, вписанных в основания. Так что ОК=r₁ и О₁K₁ = r₂.

Тогда в прямоугольном ΔКК₁Н: КН = ОК ОН = O₁K₁= r₁ r₂ и по теореме Пифагора:

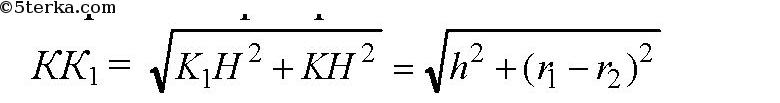
апофема.

Площадь полной поверхности равна сумме площадей S₁ и S₂

оснований и площади боковой поверхности

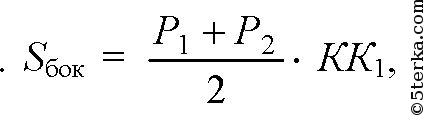
где Р₁ и Р₂ — периметры оснований. Тогда:

1) В треугольной пирамиде

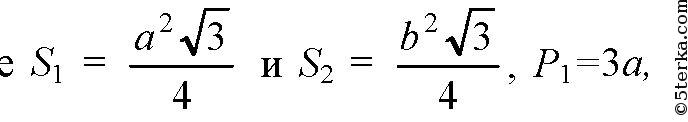
2) В четырехугольной пирамиде

Так что

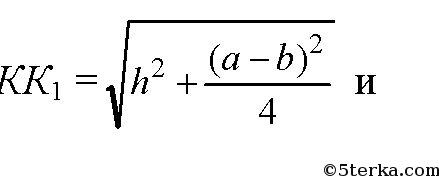
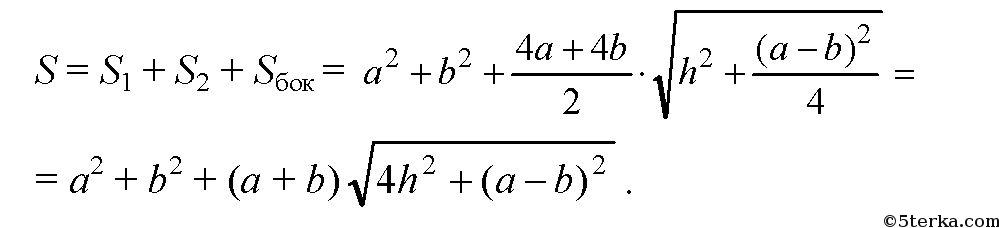
3) В шестиугольной пирамиде

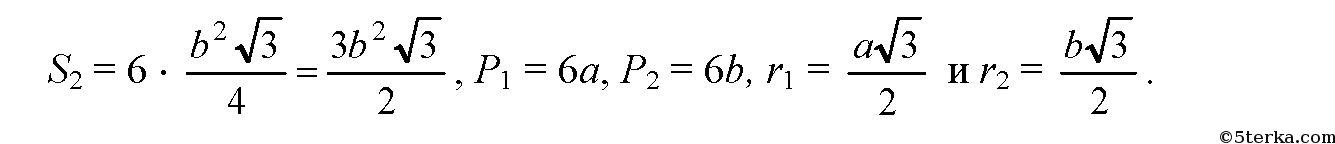
Так что