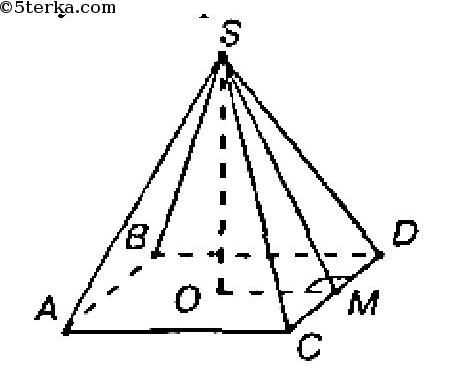
Высота SO правильной четырехугольной пирамиды проходит через центр пересечения диагоналей AD и ВС.
Проведем SM1 DC. Тогда по теореме о трех перпендикулярах OM &pepr; DC.
Значит, ОМ — радиус окружности, вписанной в квадрат, поэтому
В равнобедренном
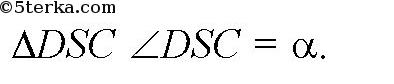
Высота SM является медианой и биссектрисой, так что
Так как ∠SMO является линейным углом двугранного угла, образованного плоскостью основания и боковой гранью, то ∠SMO=x и из ΔSMO:
Так что
Источник:
Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №58
к главе «§ 20. Многогранники».
Комментарии