
Пусть перпендикулярные плоскости α и β пересекаются по прямой с. Проведем перпендикуляры АВ, AD, АС. Тогда четырехугольник
ABCD — прямоугольник.

AC — искомое расстояние.
Осталось доказать, что точки А, В, С, D лежат в одной плоскости.
ВС — проекция АС на плоскость α, поэтому по теореме о трех перпендикулярах ВС ⊥ с, ВС ⊥ β (задача 58). Так как AD ⊥ β, то по теореме 18.4 прямые AD||BC а, значит, AD и BC лежат в одной плоскости. Что и требовалось доказать.
Так что
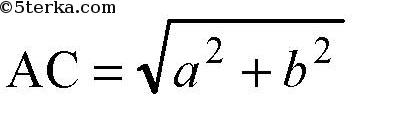
Источник:
 Решебник
по
геометрии
за 10 класс (А.В. Погорелов, 2001 год),
Решебник
по
геометрии
за 10 класс (А.В. Погорелов, 2001 год),
задача №60
к главе «§17. Перпендикулярность прямых и плоскостей».
Комментарии