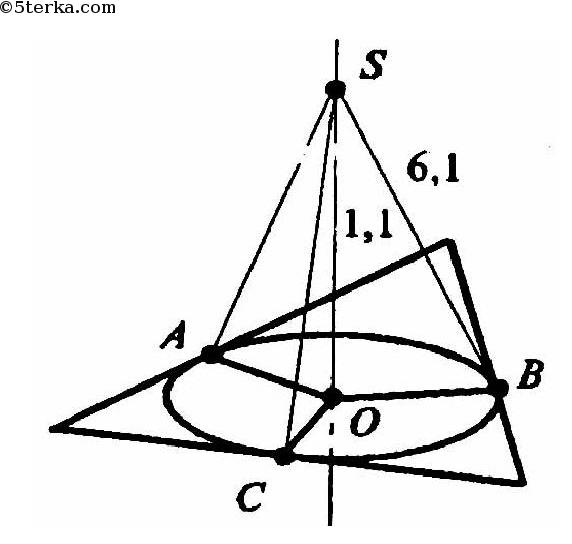
Пусть S — данная точка, и SO - перпендикуляр.Тогда SO = 1,1 м, расстояние от данной точки до плоскости треугольника. SB, SC, SA — наклонные; перпендикуляры к сторонам треугольника. Тогда АО = ВО = СО как проекции равных наклонных. По теореме о трех перпендикулярах АО, ВО, СO перпендикулярны сторонам треугольника. Значит O - центр вписанной окружности в треугольник и r = AO = OB = OC.
По теореме Пифагора в треугольнике SOB:
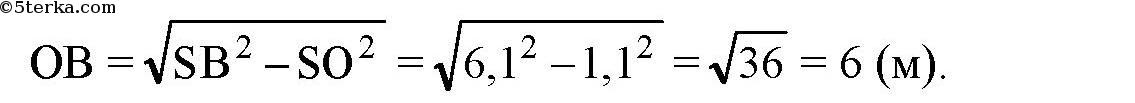
Источник:
 Решебник
по
геометрии
за 10 класс (А.В. Погорелов, 2001 год),
Решебник
по
геометрии
за 10 класс (А.В. Погорелов, 2001 год),
задача №47
к главе «§17. Перпендикулярность прямых и плоскостей».
Комментарии