41. Из вершины квадрата восстановлен перпендикуляр к его плоскости. Расстояния от конца этого перпендикуляра до других вершин квадрата равны а и b (а < b). Найдите длину перпендикуляра и сторону квадрата.

Пусть SA - данный перпендикуляр. Тогда SB = SD = а (так как равные наклонные имеют равные проекции). АВ ⊥ ВС (стороны квадрата). SB ⊥ ВС (по теореме о трех перпендикулярах).

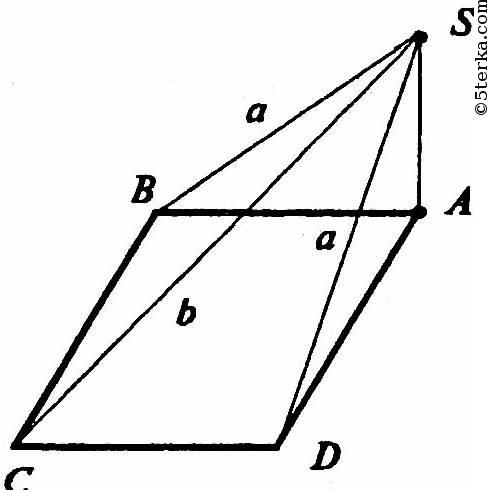
Значит, ΔSBC — прямоугольный, поэтому по теореме Пифагора: ВС2 = SC2 - SB2 = b2 - а2, так что

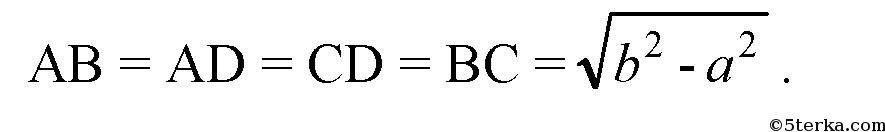
SA ⊥ AB (по условию), так что

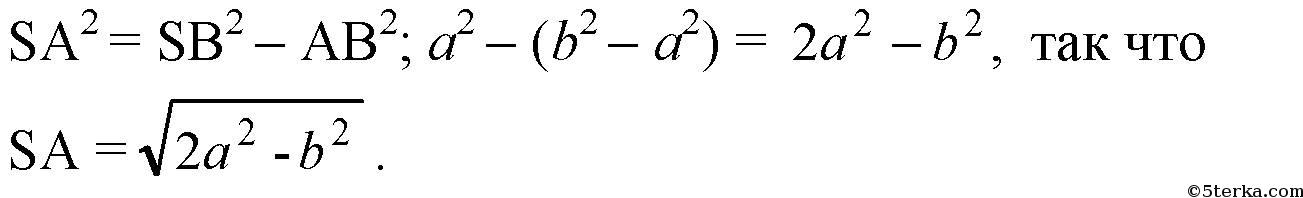
Источник:

Домашняя работа по геометрии за 10 класс к учебнику «Геометрия. 10-11 класс» А.В. Погорелов Решебник по геометрии за 10 класс (А.В. Погорелов, 2001 год),
задача №41
к главе «§17. Перпендикулярность прямых и плоскостей».

Все задачи

← 40. Через сторону параллелограмма проведена плоскость на расстоянии а от противолежащей стороны. Найдите расстояние от точки пересечения диагоналей параллелограмма до этой плоскости.
42. Из вершины прямоугольника восстановлен перпендикуляр к его плоскости. Расстояние от конца этого перпендикуляра до других вершин прямоугольника равны а, b, с (а < c, b < c). Найдите длину перпендикуляра и стороны прямоугольника. →
Комментарии