33. Концы данного отрезка, не пересекающего плоскость, удалены от нее на 0,3 м и 0,5 м. Как удалена от плоскости точка, делящая данный отрезок в отношении 3 : 7?

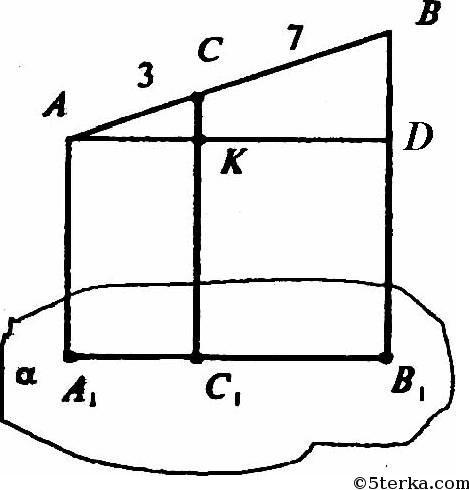
Пусть АВ — данный отрезок, С — точка на нем, такая что АС : СВ = 3 : 7.

АА₁, СС₁, ВВ₁ — перпендикуляры, опущенные из точек А, С, В на плоскость α АА₁ = 0,3м, ВВ₁ = 0,5м.

По теореме 18.4 отрезки АА₁, ВВ₁, СС₁ параллельны, и значит, лежат в одной плоскости. Точки А₁, С₁, В₁ лежат на прямой пересечения этой плоскости с плоскостью а.

Проведем из точки А прямую AD параллельную А₁В₁, значит AD ⊥ BB₁. Тогда АА₁С₁К — прямоугольник. Так что КС₁ = АА₁ DB₁=0,3 м.

ΔАСК ~ ΔABD так как СК параллельна BD. Далее