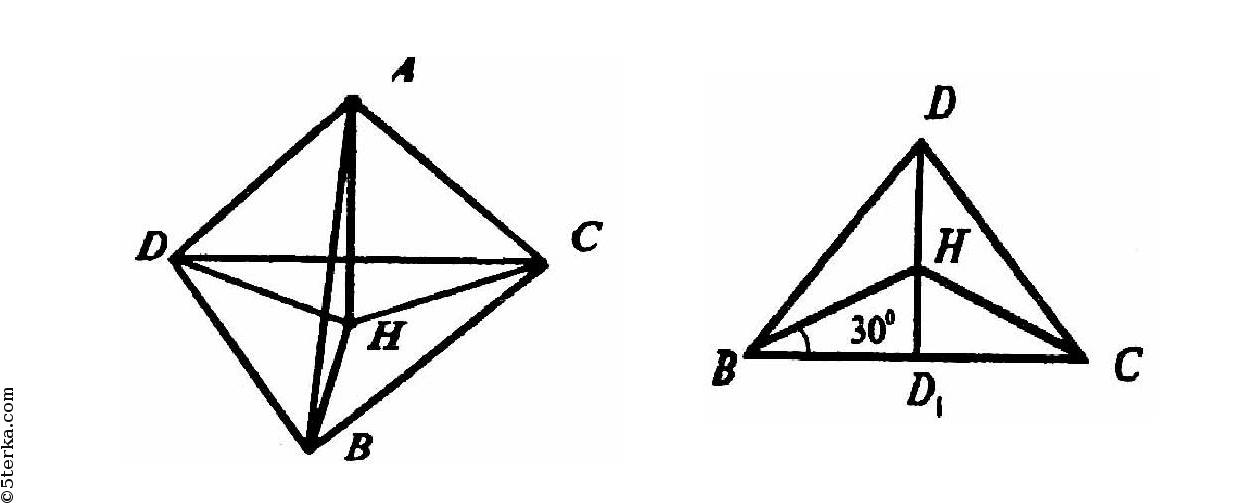
17. Точка А находится на расстоянии а от вершин равностороннего треугольника со стороной а. Найдите расстояние от точки А до плоскости треугольника.

Пусть ΔBCD — равносторонний. Проведем АН ⊥ (BCD). Так как АВ = АС = AD = а, то проекции наклонных также равны, то есть:

НВ = НС = HD.

Значит, Н — центр описанной около ΔBCD окружности, радиус

которой

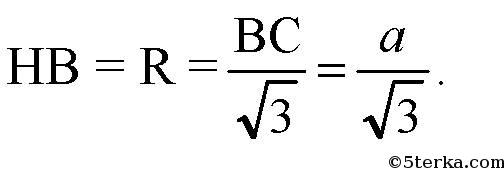
Далее так как АН ⊥ (BCD), то треугольник АНВ прямоугольный.

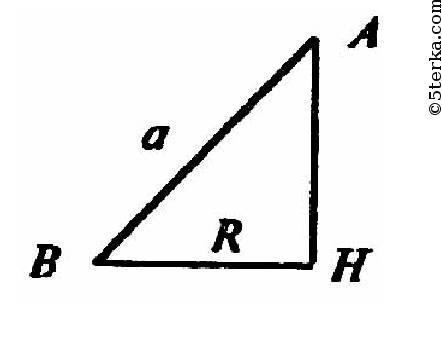
И по теореме Пифагора получаем:

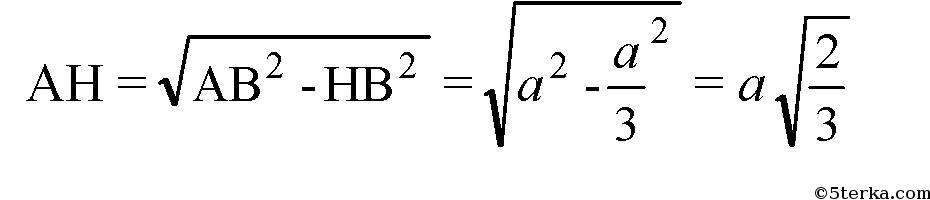
Источник:

Решебник по геометрии за 10 класс (А.В. Погорелов, 2001 год),
задача №17
к главе «§17. Перпендикулярность прямых и плоскостей».

Все задачи

← 16. Телефонная проволока длиной 15 м протянута от телефонного столба, где она прикреплена на высоте 8 м, от поверхности земли, к дому, где ее прикрепили на высоте 20 м. Найдите расстояние между домом и столбом, предполагая, что проволока не провисает.

18. Из точки S вне плоскости α проведены к ней три равные наклонные SA, SB, SC и перпендикуляр SO. Докажите, что основание перпендикуляра О является центром окружности, описанной около треугольника АВС. →

Комментарии