№ 74*. 1). В треугольнике АВС проведены медианы AA1 и BB1, которые пересекаются в точке М. В треугольнике АМВ проведена средняя линия PQ. Докажите, что четырехугольник A1B1PQ — параллелограмм. 2) Докажите, что любые две медианы треугольника в точке пересе

№ 74*. 1). В треугольнике АВС проведены медианы AA₁ и BB₁, которые пересекаются в точке М. В треугольнике АМВ проведена средняя линия PQ. Докажите, что четырехугольник A₁B₁PQ — параллелограмм. 2) Докажите, что любые две медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины. 3) Докажите, что все три медианы треугольника пересекаются в одной точке.

1) Так как PQ — средняя линия

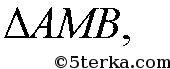
то

и

— средняя линия

поэтому

и

Так как

и

то

А так же

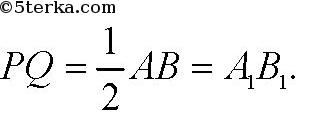
Значит, четырехугольник

— параллелограмм, так как две его стороны параллельны и равны, чем доказано первое утверждение. 2) Докажем, что медианы

в точке пересечения делятся в отношении 2:1, считая от вершины.

средняя линия

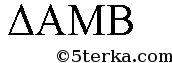
, следовательно

Выше мы доказали, что

— параллелограмм, значит, его диагонали в точке пересечения делятся пополам, то есть

и

Получаем

Чем доказано второе утверждение задачи. 3) Проведем третью медиану

_, которая пересекает медиану

в некоторой точке и, согласно доказанному во второй части задачи, эта точка должна делить медиану

в отношении 2:1, считая от точки А. Так как положение такой точки на отрезке определяется однозначно, то она совпадает с точкой М. Значит, СС₁ проходит через точку М. То есть все три медианы пересекаются в одной точке. Что и требовалось доказать.