№ 58. Докажите, что середины сторон прямоугольника являются вершинами ромба. И наоборот, середины сторон ромба являются вершинами прямоугольника.

1) Четырехугольник ABCD — прямоугольник, Е, F, К и H— середины его сторон. Четырехугольник EFKH — параллелограмм (см. решение задачи № 55).

(так как ЕВ=СК и ВF=FC). Значит EF = FK, где EF и FK - стороны параллелограмма. Значит, EFKH — ромб. 2) Пусть четырехугольник ABCD является ромбом и Е, F, К, H — середины его сторон.

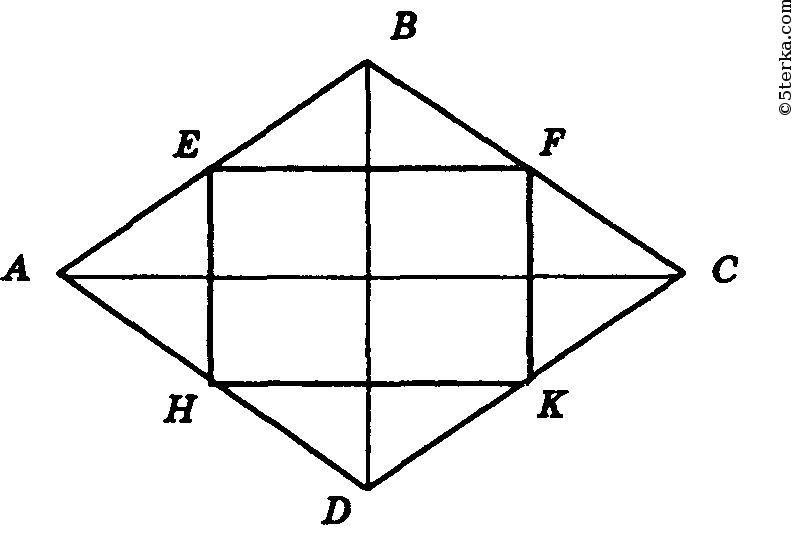
Четырехугольник EFKH — параллелограмм (см. задачу №55). Его стороны параллельны диагоналям ромба (как средние линии), а они перпендикулярны, значит, углы четырехугольника EFKH — прямые. Значит, четырехугольник EFKH — прямоугольник. Что и требовалось доказать.