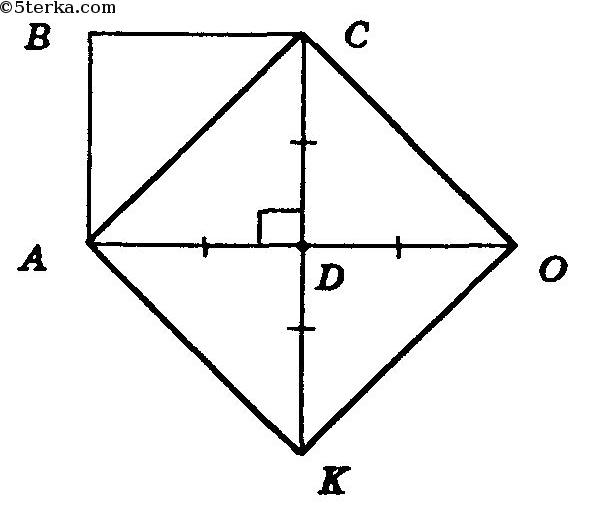
Пусть в квадрате ABCD сторона АВ = 1м. Продолжим сторону АD и на продолжении от точки D, отложив отрезок DO = AD, аналогично продолжим CD, отложив отрезок DK = CD. Получим четырехугольник АСОК, в котором диагонали АО и СК в точке пересечения делятся пополам, а также равны и взаимно перпендикулярны, значит, АСОК — квадрат, диагонали которого
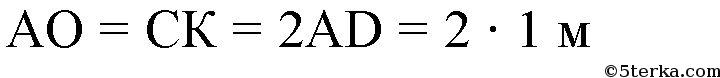
= 2 м. Ответ:
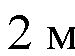
Источник:
Решебник
по
геометрии
за 8 класс (А.В. Погорелов, 2001 год),
задача №44
к главе «§ 6. Четырехугольники».
Комментарии