№ 42. Дан квадрат ABCD. На каждой из его сторон отложены равные отрезки AA1=BB1=CC1=DD1. Докажите, что четырехугольник A1B1C1D1 есть квадрат.

№ 42. Дан квадрат ABCD. На каждой из его сторон отложены равные отрезки AA₁=BB₁=CC₁=DD₁. Докажите, что четырехугольник A₁B₁C₁D₁ есть квадрат.

Рассмотрим

(по условию). А значит и

(т.к. ABCD — квадрат). Тогда,

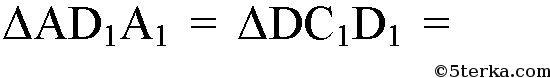
(по двум катетам). Значит,

а также

∠AD₁A₁ + ∠AA₁D₁ = 90° (сумма острых углов прямоугольного треугольника). Значит,

А так как

Аналогично доказывается, что и остальные углы четырехугольника

прямые. Тогда, данный четырехугольник

является квадратом. Что и требовалось доказать.