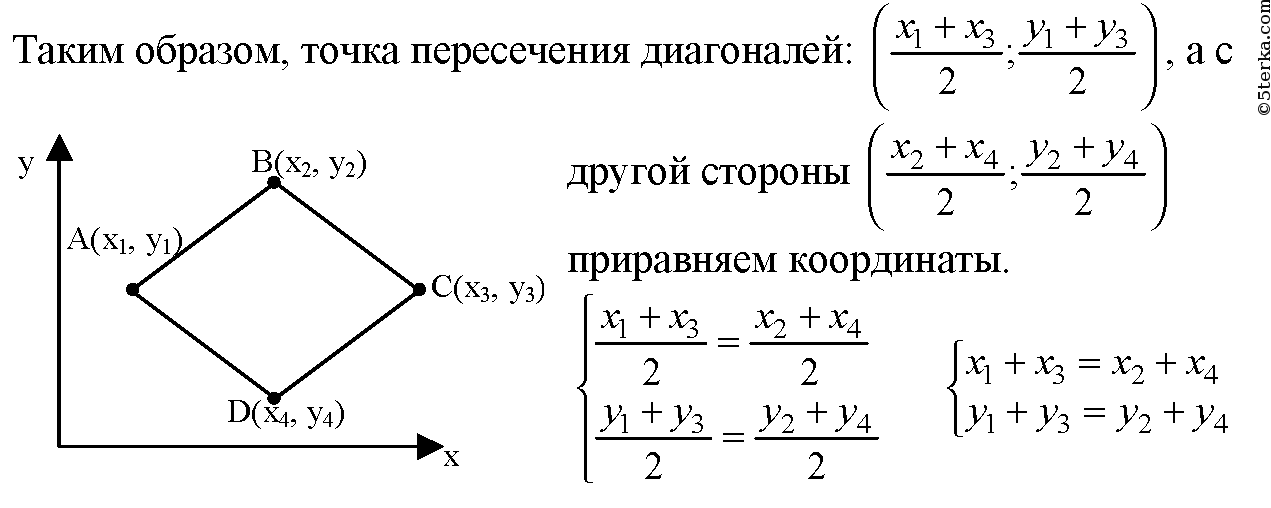
1256 Вершины четырехугольника ABCD имеют координаты А (х1; у1), В (х2; у2), С (х3; у3) и D (х4; y4). Докажите, что этот четырехугольник является параллелограммом тогда и только тогда, когда х1+ х3= х2+ х4 и y1+ y3=y2+y4.
По признаку параллелограмма (если диагонали четырехугольника точкой пересечения делятся пополам, то это - параллелограмм).
Источник:
 Решебник
по
геометрии
за 9 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
Решебник
по
геометрии
за 9 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №1256
к главе «Задачи повышенной трудности. Задачи к главе X».
Комментарии