1136 Квадрат А1А2А3А4 вписан в окружность радиуса R (рис. 320). На его сторонах отмечены восемь точек так, что A1B1=A2B2=A3B3=A4B4=A1C1=A2C2= A3C3 = A4C4= R. Докажите, что восьмиугольник B1C3B2C4B3C1B4C2 правильный, и выразите площадь этого восьмиугольника через радиус R.


Дано:

Доказать:

Доказательство:
Докажем, что все стороны равны:
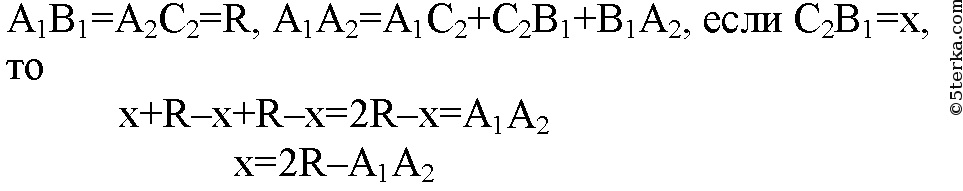
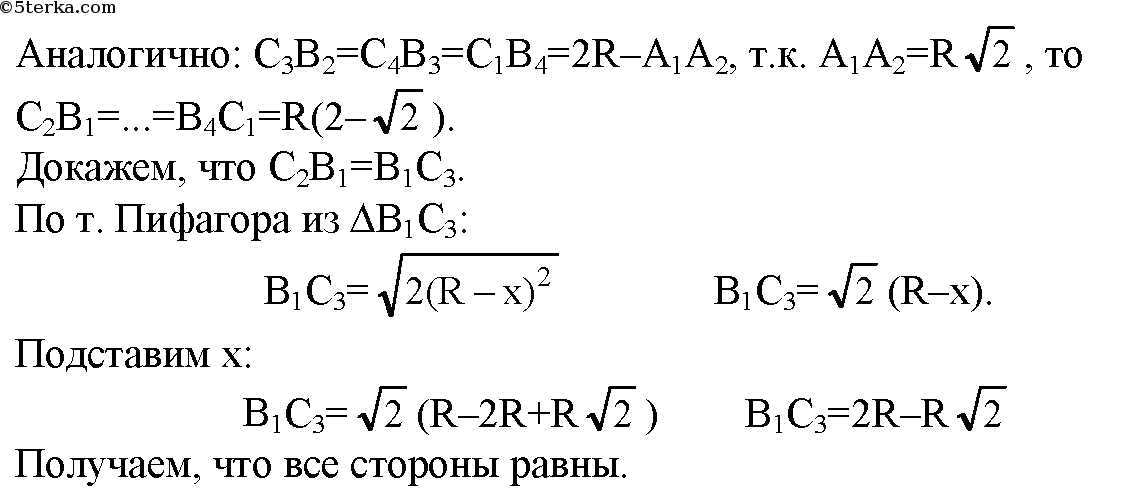


Источник:
 Решебник
по
геометрии
за 9 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
Решебник
по
геометрии
за 9 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №1136
к главе «Глава XII. Длина окружности и площадь круга. Дополнительные задачи».
Комментарии