Решение. Если данный четырехугольник выпуклый, то согласно задаче 814 его диагонали пересекаются, поэтому любые две противоположные вершины четырехугольника лежат по разные стороны от прямой, проходящей через две другие вершины.
Пусть ABCD — невыпуклый четырехугольник. Тогда одна из прямых, содержащих сторону четырехугольника, например прямая АВ, пересекает сторону CD в некоторой точке М. Отрезки АВ и CD не пересекаются, поэтому возможны два случая:
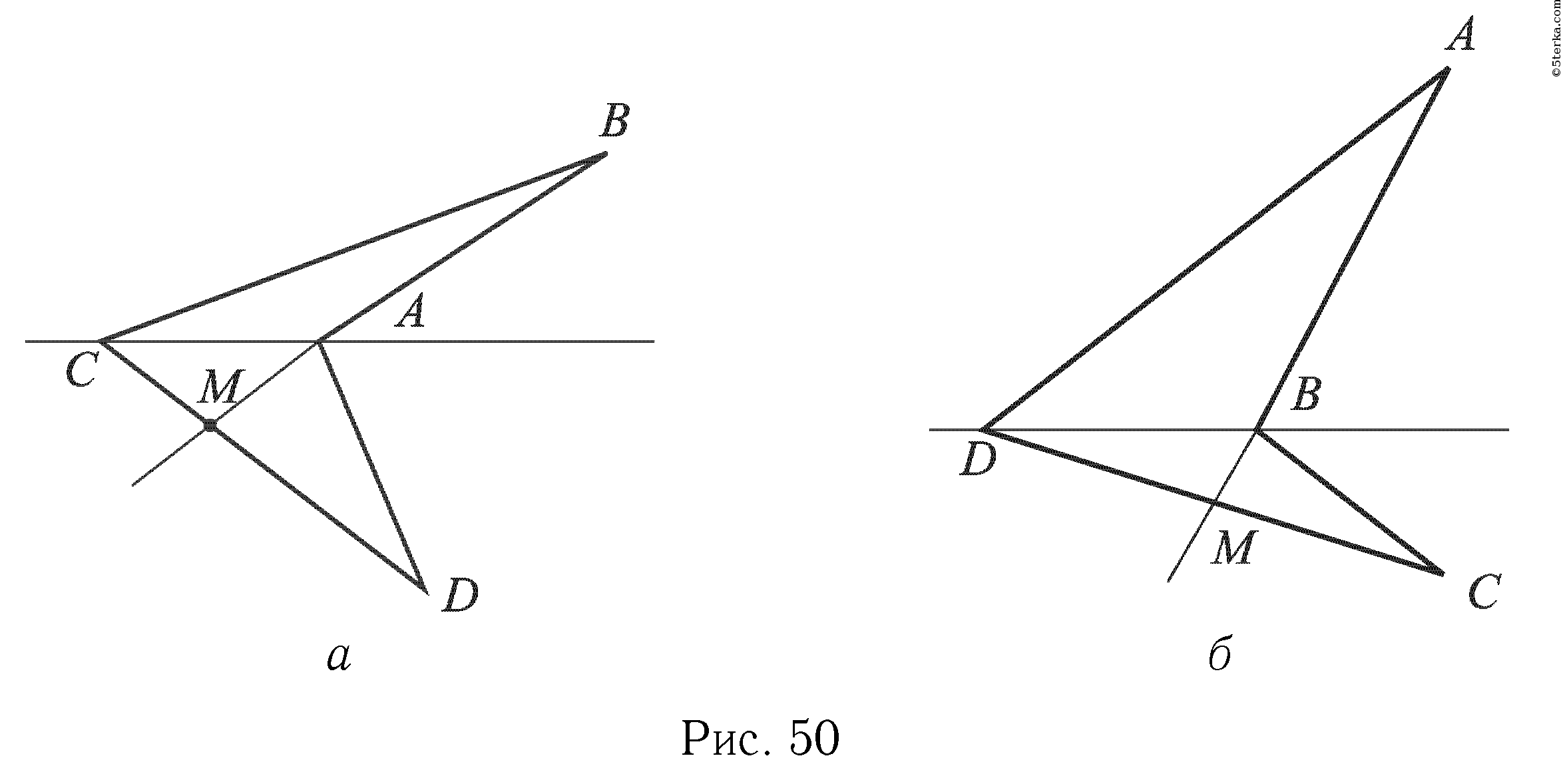
а) Точка А лежит на отрезке ВМ (рис. 50, а). В этом случае точки В и М лежат по разные стороны от прямой АС. Отрезок MD не пересекается с прямой АС, поэтому точка D лежит по ту же сторону от прямой АС, что и точка М. Итак, вершина В лежит по одну сторону от прямой АС, а противоположная вершина D — по другую сторону от этой прямой.
б) Точка В лежит на отрезке AM (рис. 50, б). Аналогично случаю а) можно доказать, что противоположные вершины А и С лежат по разные стороны от прямой BD.
Решебник
по
геометрии
за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №815
к главе «Глава V. Четырехугольники. Задачи повышенной трудности».