788 Дан произвольный треугольник ABC. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника ABC.

Решение

Пусть AA1, BB1, СС1 — медианы треугольника ABC. Тогда

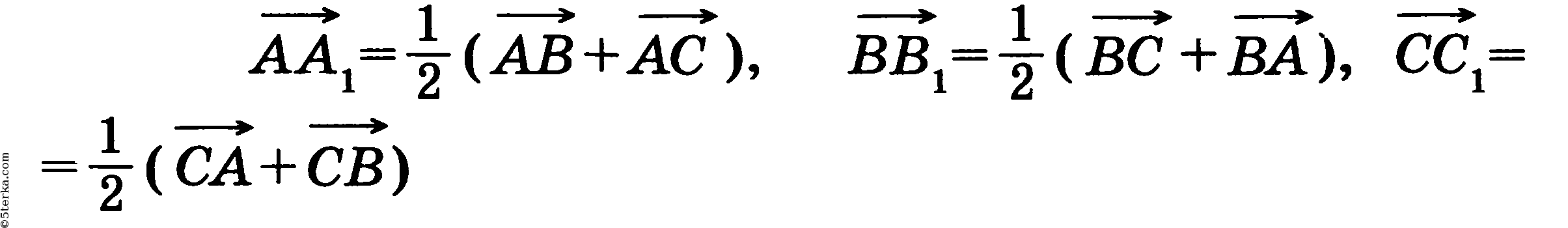
(см. задачу 1, п. 84). Сложив эти равенства, получим

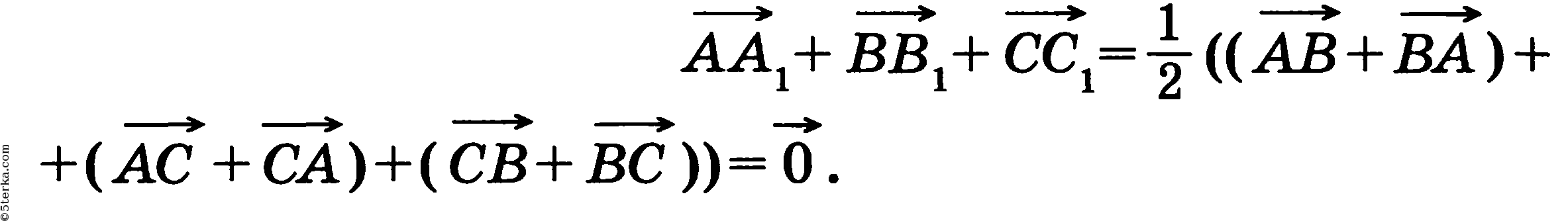
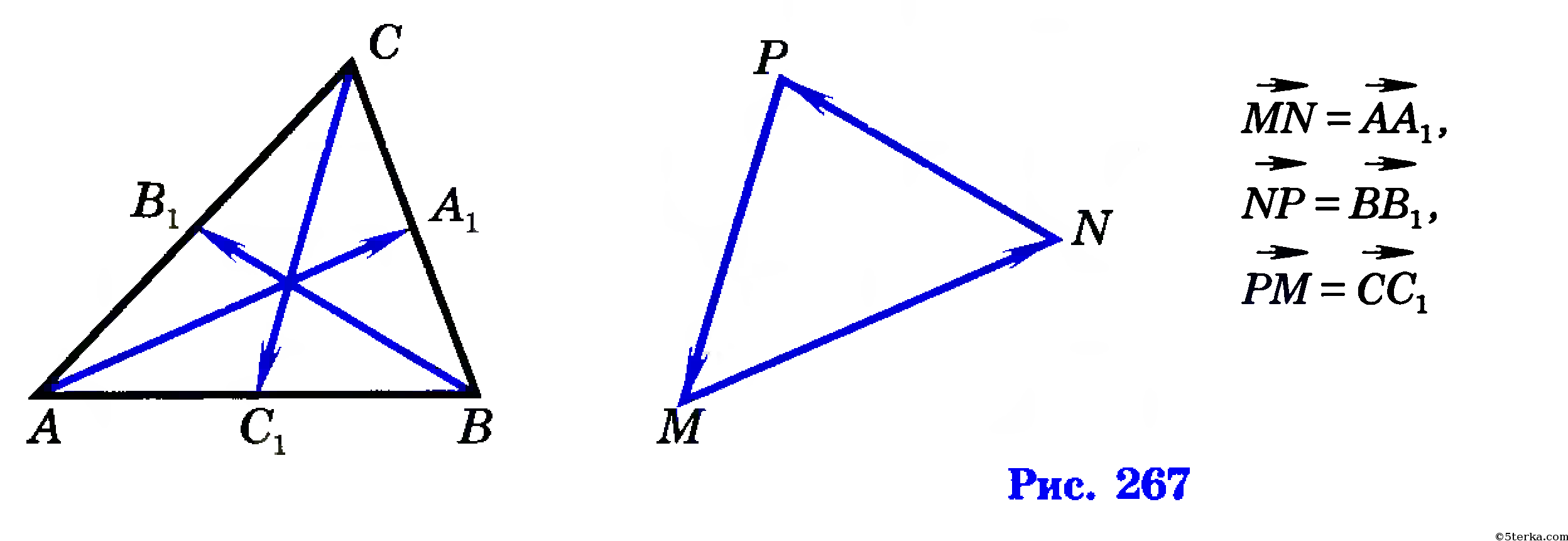
Отсюда следует, что если мы построим сумму векторов AA1, BB1, СС1 по правилу многоугольника (п. 81), то получим треугольник, удовлетворяющий условиям задачи (треугольник MNP на рисунке 267).

Источник:

Решебник по геометрии за 8 класс к учебнику Геометрия. 7-9 класс Л.С.Атанасян и др. Решебник по геометрии за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №788
к главе «Глава IX. Векторы. §3. Умножение вектора на число.».

Все задачи

← 787 Точка О — середина медианы EG треугольника DEF. Выразите вектор DO через векторы a=ED и b =EF.
789 На сторонах треугольника ABC построены параллелограммы АВВ1А2, ВСС1В2, ACC2A1. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны отрезкам А1А2, В1В2 и C1C2. →
Комментарии