729* Докажите, что если в четырехугольнике сумма противоположных углов равна 180°, то около этого четырехугольника можно описать окружность.

Решение

Пусть в четырехугольнике ABCD

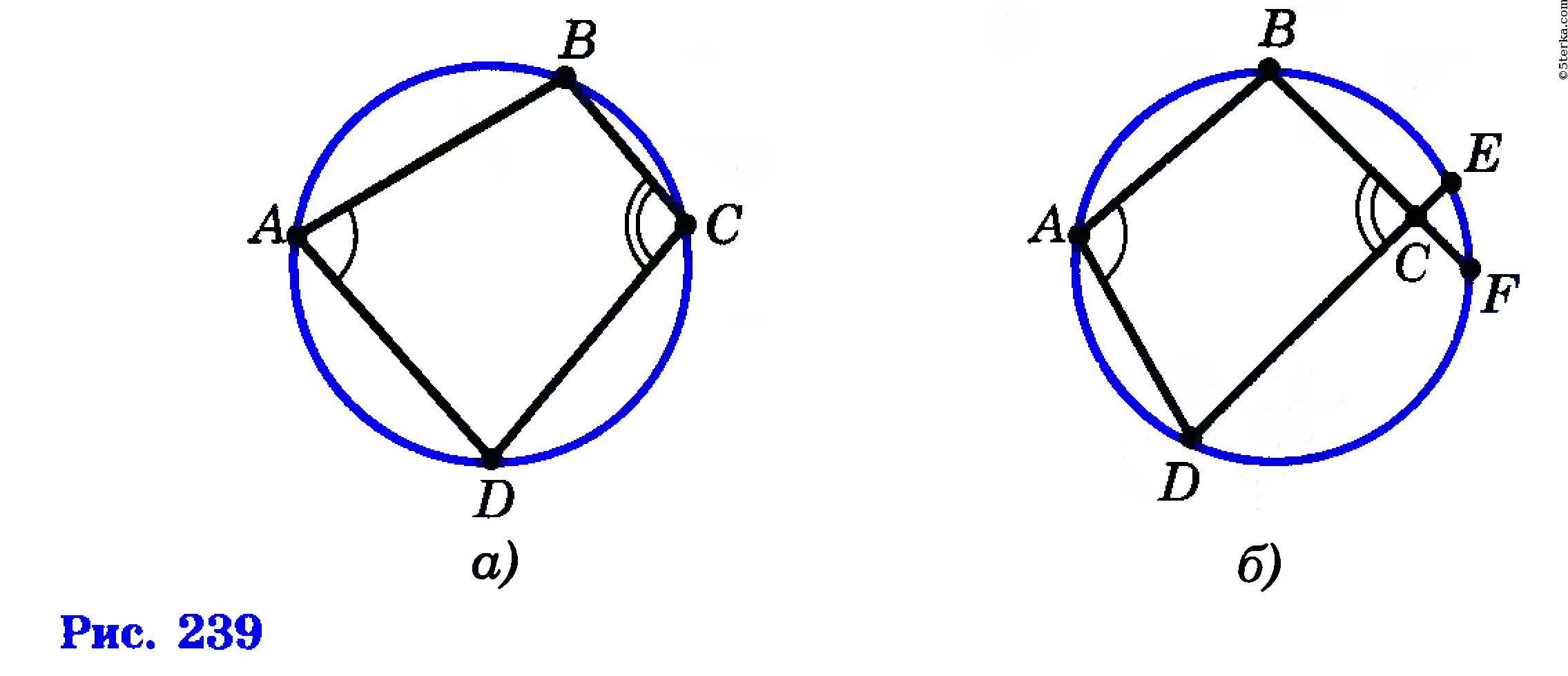
Итак, мы получили, что ∠A+∠C > 180°. Но это противоречит условию (1), и, значит, наше предположение ошибочно. Аналогично можно доказать (опираясь на задачу 719), что вершина С не может лежать вне круга. Следовательно, вершина С лежит на окружности, что и требовалось доказать.

Источник:

Решебник по геометрии за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №729
к главе «Глава VIII. Окружность. Дополнительные задачи».

Все задачи

← 728 Докажите, что если около ромба можно описать окружность, то этот ромб — квадрат.

730 Через точки А и В проведены прямые, перпендикулярные к сторонам угла АОВ и пересекающиеся в точке С внутри угла. Докажите, что около четырехугольника АСВО можно описать окружность. →

Комментарии