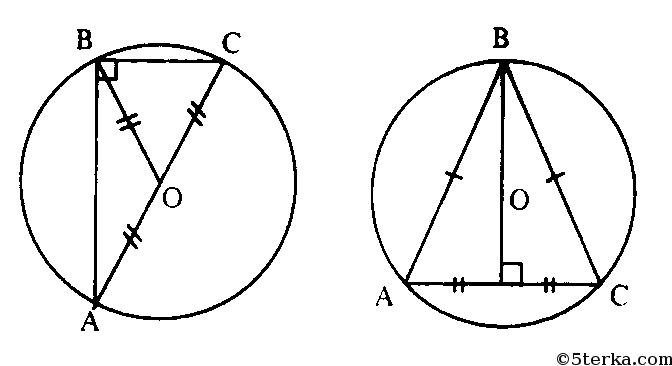
Дано:
Доказать: ΔABC -равнобедренный или прямоугольный
Доказательство:
Центр окружности, описанной около треугольника, лежит на
пересечении серединных перпендикуляров к сторонам ΔАВС. Т.к.
О ∈ медиане, значит медиана и серединный перпендикуляр совпадают, т.е. треугольник равносторонний или равнобедренный (одна из медиан является серединным перпен-
дикуляром к основанию).
О - лежит на гипотенузе прямоугольного треугольника ВО = АО = ОС.
Источник:
Решебник
по
геометрии
за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №726
к главе «Глава VIII. Окружность. Дополнительные задачи».
Комментарии