384 Через середину М стороны АВ треугольника ABC проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN=NC.

Решение

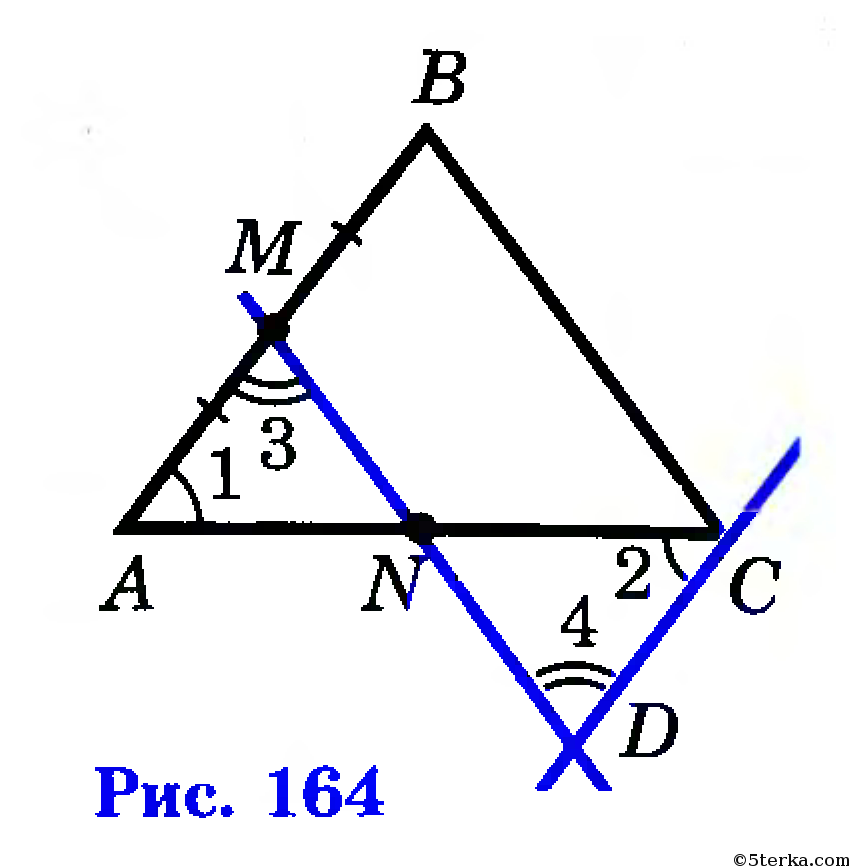
Через точку С проведем прямую, параллельную прямой АВ, и обозначим буквой D точку пересечения этой прямой с прямой MN (рис. 164). Так как АМ=МВ по условию, a MB=CD как противоположные стороны параллелограмма BCDM, то AM=DC. Треугольники AMN и CDN равны по второму признаку равенства треугольников (AM=CD, ∠1=∠2 и ∠3=∠4 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущими АС и MD), поэтому AN=NC.