781. Дан куб ABCDA1B1C1D1. Докажите, что пересечение тетраэдров AB1CD1 и C1BA1D есть правильный октаэдр.

Пересечение тетраэдров AB₁CD₁ и C₁BAD есть многогранник с вершинами в центрах M, N, К, L, Р, Q граней куба, то есть октаэдр.

Например, его грань MNP ограничена отрезками

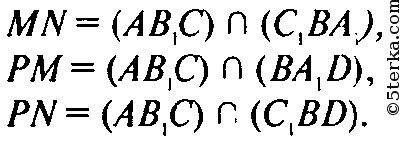
Октаэдр — правильный: он

выпуклый, грани его —

правильные треугольники со

стороной

где а — ребро куба, и

в каждой вершине сходится четыре ребра.

Источник:

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №781
к главе «Задачи повышенной трудности».

Все задачи

← 780. Какую наибольшую длину может иметь ребро правильного тетраэдра, который помещается в коробку, имеющую форму куба со стороной 1 см?

782. Докажите, что из конечного числа попарно различных кубов нельзя составить прямоугольный параллелепипед. →

Комментарии