779. Площадь боковой грани правильной шестиугольной пирамиды равна S. Найдите площадь сечения пирамиды плоскостью, проходящей через середину высоты пирамиды и параллельной плоскости боковой грани.

Плоскость сечения проходит через середину О, высоты РО правильной пирамиды PABCDEF и параллельна плоскости грани РАВ. Она пересекает плоскость основания по прямой А₁В₁ || АВ, плоскость PFC по прямой F₁C₁ || А₁В₁ и плоскость PED по прямой

E₁D₁||A₁B₁.

Пусть

то

гда

По условию

где

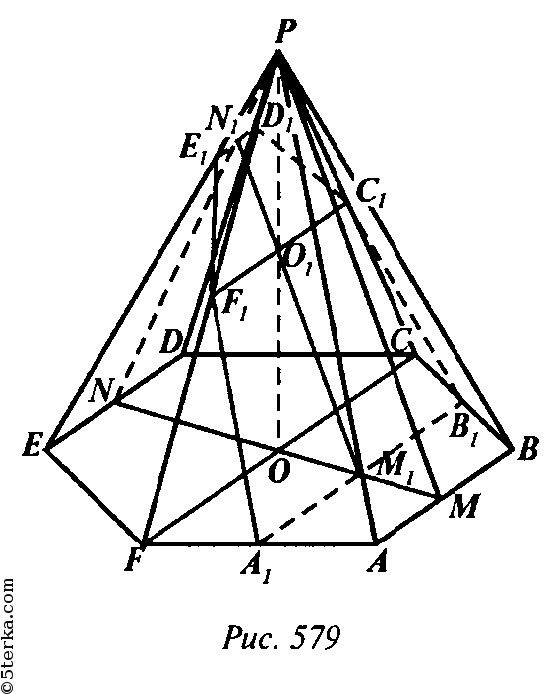
Так как О₁ - середина РО, то M₁,A₁,B₁ — соответственно середины ОМ, AF, ВС, FC = 2а,

Так как

то

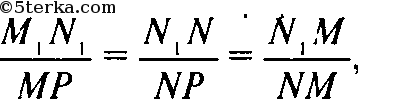
то есть

откуда

Т. к.

и

то

откуда

Следовательно,

(3)

Из (2), (3) и (1)

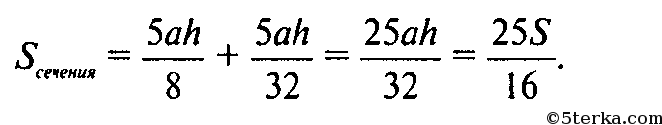
Источник:

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №779
к главе «Задачи повышенной трудности».

Все задачи

← 778. Докажите, что в кубе можно вырезать сквозное отверстие, через которое можно протащить куб таких же и даже больших размеров.

780. Какую наибольшую длину может иметь ребро правильного тетраэдра, который помещается в коробку, имеющую форму куба со стороной 1 см? →

Комментарии