775. Докажите, что сумма квадратов расстояний от вершин куба до прямой, проходящей через его центр, не зависит от положения этой прямой.

Пусть A₁A₂...A₈ — данный куб с ребром а, р — прямая, проходящая через его центр О,

Так как

то

Если

а х, у —

координаты в системе с осями А₁А₂ и А₁А₄, то

По теореме косинусов из ΔOPA_i имеем

где

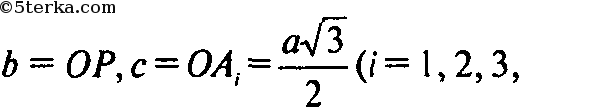
причем

Приравняв выражения для

получим из найденных

равенств:

Отсюда после вычислений получаем:

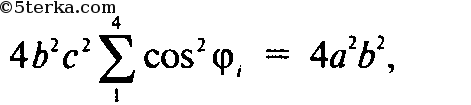
тогда из (1)

Таким образом, s не зависит от положения прямой р.