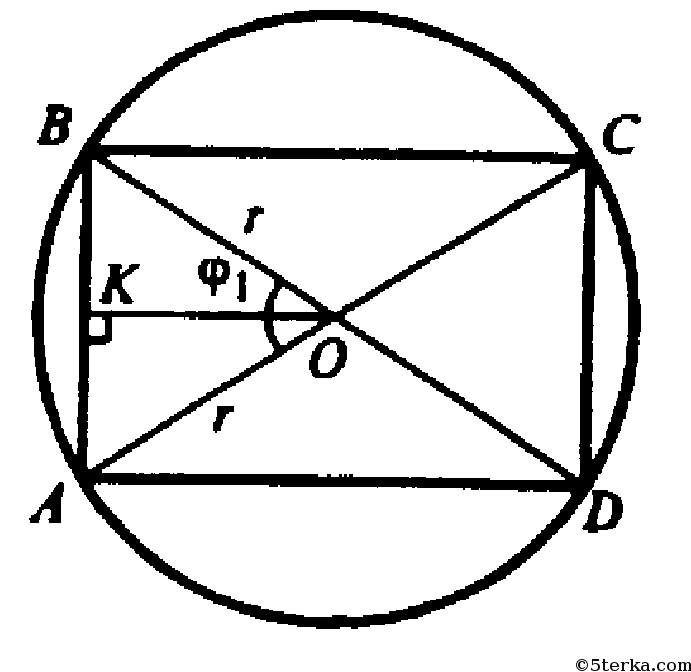
748. В конус вписана пирамида, основанием которой является прямоугольник. Меньшая сторона прямоугольника равна a, a острый угол между его диагоналями равен φ1. Боковая грань, содержащая меньшую сторону основании, составляет с плоскостью основания двугранный угол φ2. Найдите объем конуса.
Пусть РО — это высота конуса, РО=Н, АВ<AD. Построим ОК⊥АВ, отрезок РК. По теореме о трех перпендикулярах РК перпендикулярно АВ.
В основании пирамиды.
АВ=а, ВО=OD=AO=OC — по свойству диагоналей прямоугольника. ВО=R.
В треугольнике АВО:
По теореме синусов запишем:
Из треугольника ВКО:
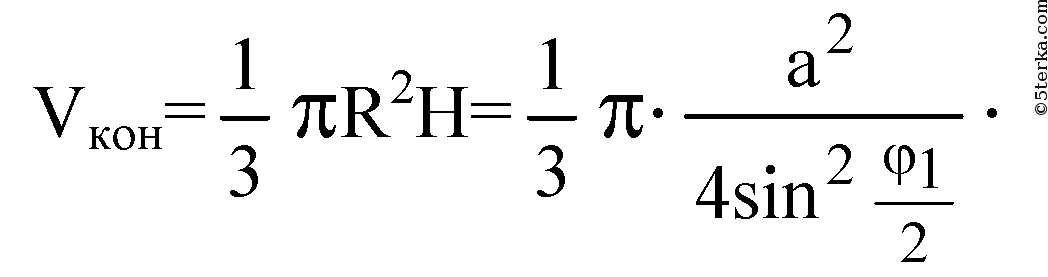
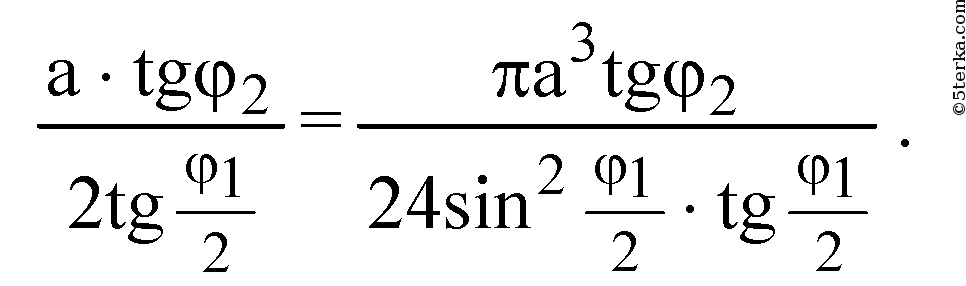
Источник:
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №748
к главе «Разные задачи на многогранники, цилиндр, конус и шар».
Комментарии