743. Два ребра тетраэдра равны b, а остальные четыре ребра равны а. Найдите объем тетраэдра, если ребра длины b: а) имеют общие точки; б) не имеют общих точек.

а) Пусть АС=АВ=b, а DA=DB=DC=BC=a. Построим высоту пирамиды DO, отрезки ОА, ОВ, ОС.

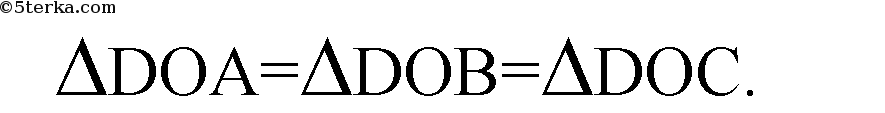
Тогда, ОА=ОВ=ОС=R, где R — радиус

окружности, описанной вокруг ΔАВС.

В равнобедренном треугольнике ΔВАС проведем из угла А высоту АК.

ОА=R по формуле

(a, b, с — стороны треугольника, S — его площадь) Вычислим площадь, вычислим R.

Из ΔADO:

б) в равнобедренном треугольнике АВС (СА=СВ=а) построим высоту СК ⊥AB; проведем отрезок DK.

В треугольнике ADB: DK — высота (ΔADB — равнобедренный, АК=КВ, значит, медиана DK является высотой).

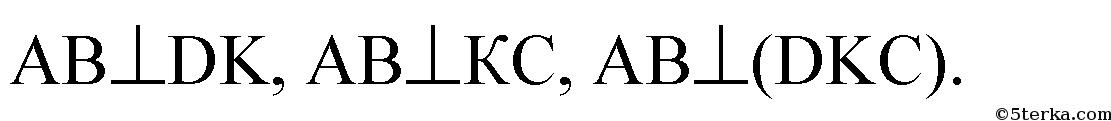
Если плоскость проходит через перпенди-куляр к другой плоскости, то она перпендикулярна к этой плоскости. Итак, плоскости АВС и DKC перпендикулярны. В плоскости DKC проведем

высоту пирамиды DO; DO⊥CK.

Примем DO=H.

В треугольнике АВС:

Вычислим высоту пирамиды:

Проведем KE⊥DC.

Из треугольника KDE: