691. Основанием пирамиды служит равнобедренный треугольник ABC, в котором АВ = ВС= 13 см, АС= 10 см. Каждое боковое ребро пирамиды образует с ее высотой угол в 30°. Вычислите объем пирамиды.

Построим SO перпендикулярно плоскости АВС; SO — это высота пирамиды. ΔSOA=ΔSOB= =ΔSOC, они прямоугольные, SO — общий катет, они имеют равный острый угол. Тогда, ОВ=ОС=ОА=R где R — радиус описанной окружности.

По теореме косинусов в треугольнике ΔАВС:

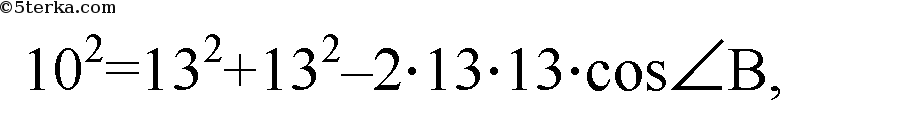
Значит,

Из треугольника ΔSOB найдем высоту SO:

Источник:

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №691
к главе «Глава VII. Объемы тел. § 3. Объём наклонной призмы, пирамиды и конуса».

Все задачи

← 690. Найдите объем и площадь боковой поверхности правильной шестиугольной пирамиды, если ее боковое ребро равно 13 см, а диаметр круга, вписанного в основание, равен 6 см.

692. Основанием пирамиды является прямоугольный треугольник с катетами a и b. Каждое ее боковое ребро наклонено к плоскости основания под углом φ. Найдите объем пирамиды. →

Комментарии