680. Основанием наклонного параллелепипеда является прямоугольник со сторонами а и b. Боковое ребро длины с составляет со смежными сторонами основания углы, равные φ. Найдите объем параллелепипеда.

Построим

(по гипотенузе и острому углу). Значит,

Построим В1О ⊥ плоскости ABC, отрезки ON и OM. Из равенства наклонных В1М и В1N следует равенство их проекций, ОМ=ОN, то есть точка О лежит на биссектрисе угла АВС.

Из ΔВ1ВМ:

Из прямоугольного ΔВ1ВО:

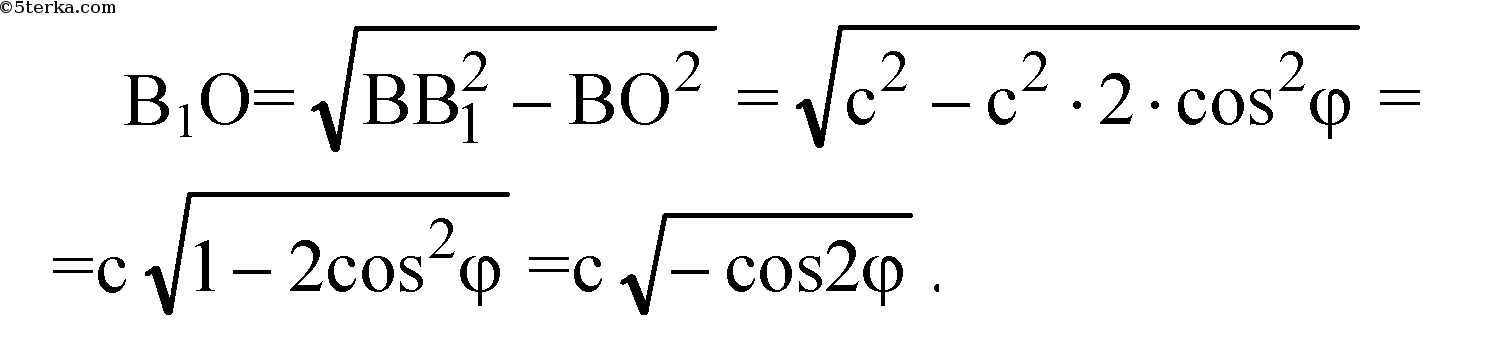
В1О — высота параллелепипеда.

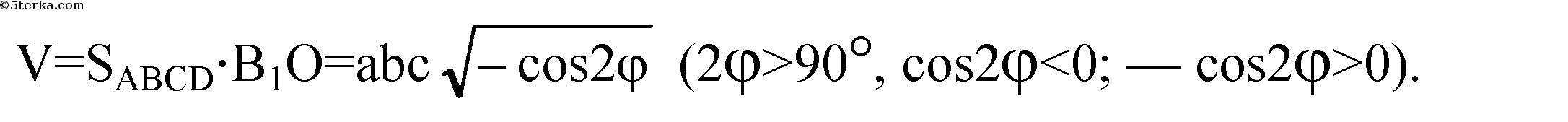
Источник:

Решебник по геометрии за 10 класс к учебнику Геометрия. 10-11 класс Л.С.Атанасян Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №680
к главе «Глава VII. Объемы тел. § 3. Объём наклонной призмы, пирамиды и конуса».

Все задачи

← 679. Основанием наклонной призмы ABCA1B1C1 является прямоугольный треугольник ABC с катетами АВ = 7 см и AC = 24 см. Вершина А1 равноудалена от вершин А, В и С. Найдите объем призмы, если ребро АА1 составляет с плоскостью основания угол в 45°.
681. Все грани параллелепипеда — равные ромбы, диагонали которых равны 6 см и 8 см. Найдите объем параллелепипеда. →
Комментарии