а) n=3, ΔАВС — правильный. Обозначим сторону ΔАВС равной х, следовательно,

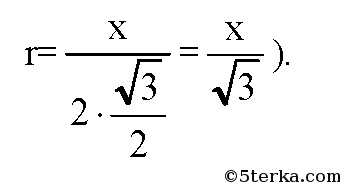
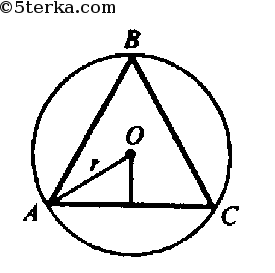


б) n=4, ABCD — квадрат. Обозначим сторону квадрата равной х.
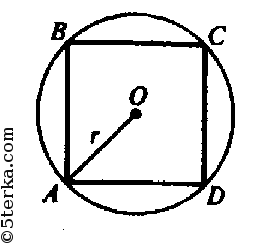


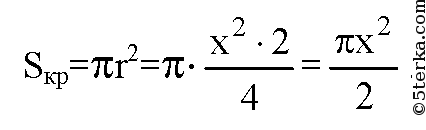

в) n=6. Обозначим сторону 6-угольника за х, следовательно, r=х.
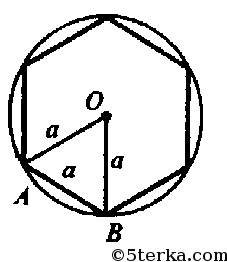
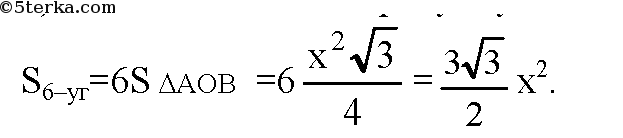
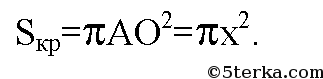

г) обозначим сторону правильного вписанного n-угольника за х. Следовательно, радиус описанной окружности равен
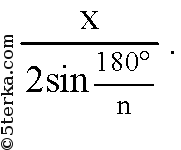
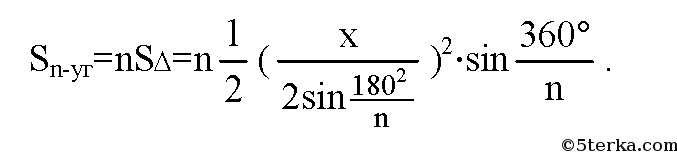
(Правильный n-угольник разбивается радиусами, проведенными из центра, на n одинаковых треугольников; все треугольники равновелики)

Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №671
к главе «Глава VII. Объемы тел. § 2. Объём прямой призмы и цилиндра».
Комментарии