621. Расстояние от центра сферы радиуса R до данной прямой равно d. Докажите, что: а) если d<R, то прямая пересекает сферу в двух точках; б) если d = R, то прямая имеет только одну общую точку со сферой; в) если d>R, то прямая не имеет со сферой ни

621. Расстояние от центра сферы радиуса R до данной прямой равно d. Докажите, что: а) если d<R, то прямая пересекает сферу в двух точках; б) если d = R, то прямая имеет только одну общую точку со сферой; в) если d>R, то прямая не имеет со сферой ни одной общей точки.

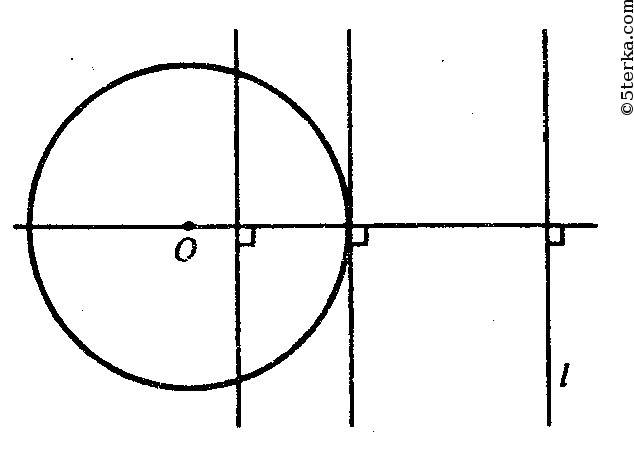
Очевидно, что из точки О всегда можно провести прямую (отрезок), перпендикулярную l. Введем систему координат, как показано на рисунке.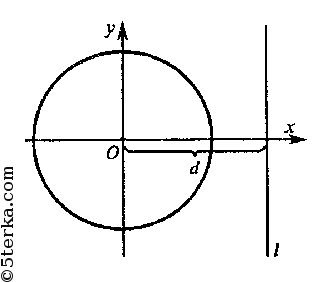

Уравнение окружности:

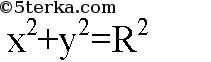
Уравнение прямой l : x=d Исследуем систему :

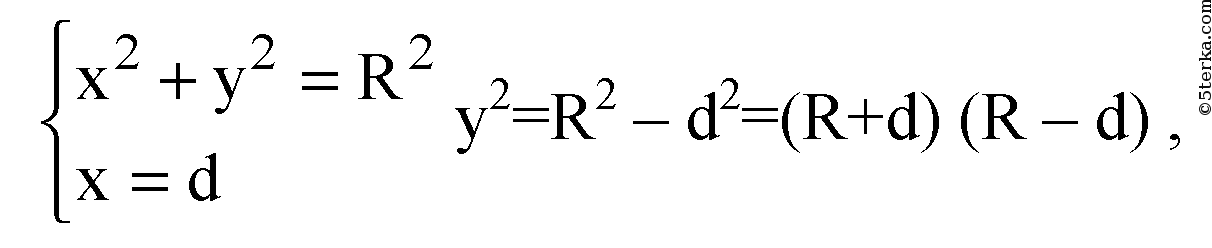
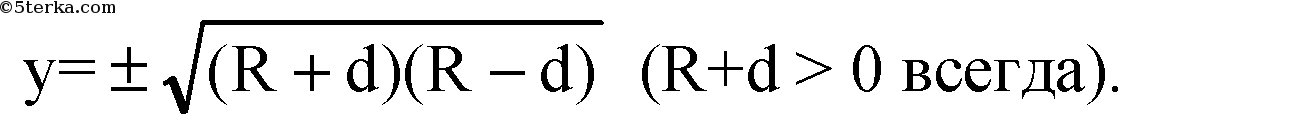
а)    Если R - d > 0, R=d и у=0 — касание в точке (d, 0) с окружностью, а значит, со сферой.

б)    Если R - d < 0, то решений нет, значит, l не пересекается с окружностью; l не пересекается со сферой.