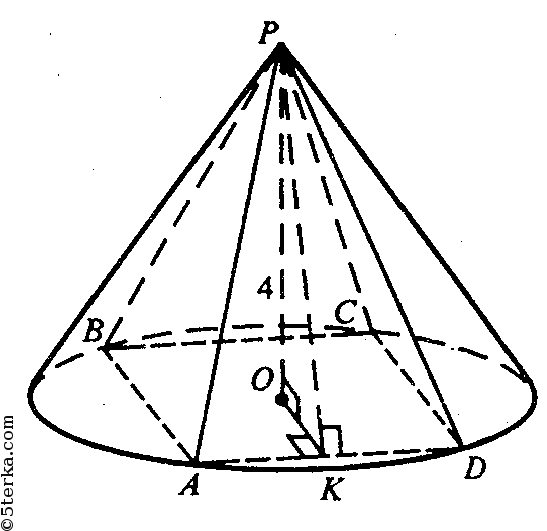
* Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина пирамиды совпадает с вершиной конуса.
а). Построим ОК ⊥ ВС, отрезок DK. По теореме о трех перпендикулярах DK⊥ВС. В правильном ΔАВС, ОК — радиус вписанной в ΔАВС окружности. Примем ОК=r.
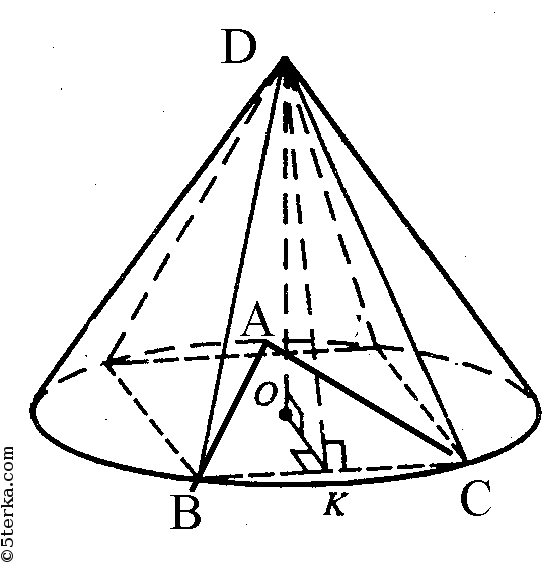
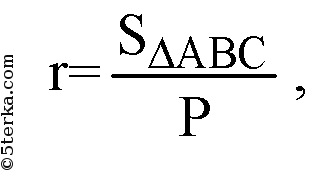
где р — полупериметр ΔАВС.
Из равенства

(теорема синусов для ΔАВС) найдем а — сторону ΔАВС
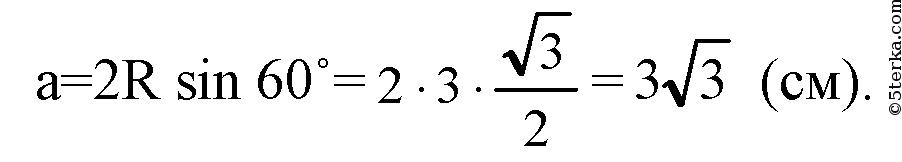
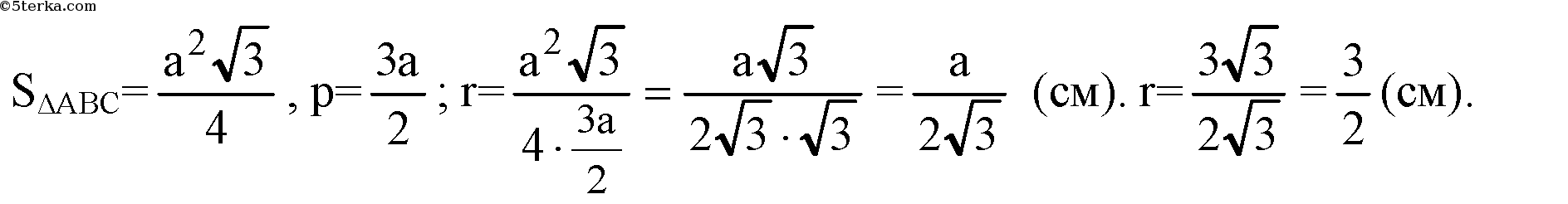
Из прямоугольного ΔDOK:
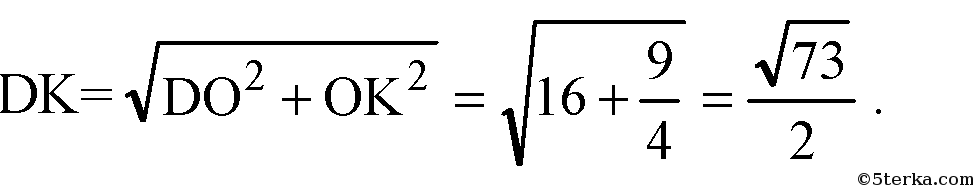
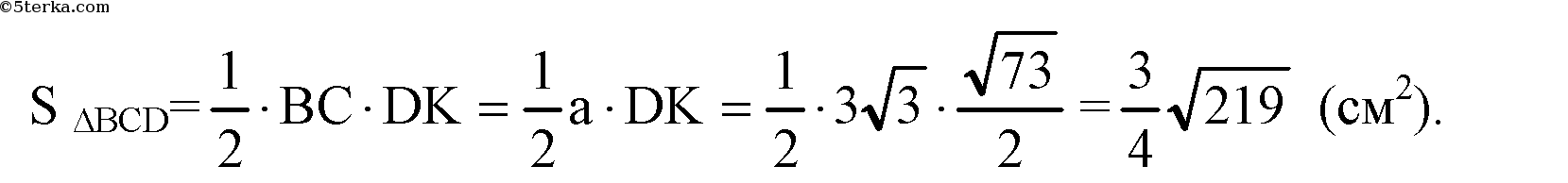
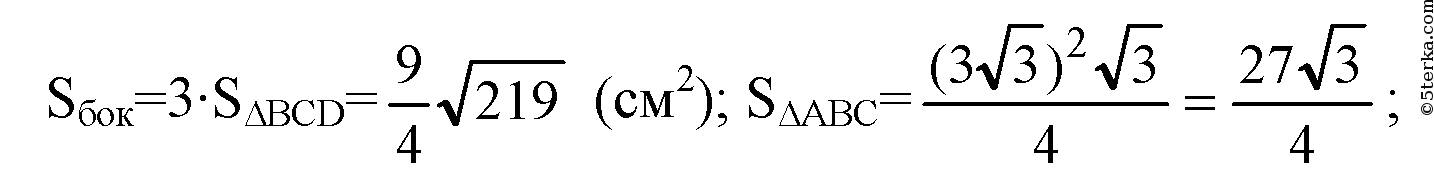
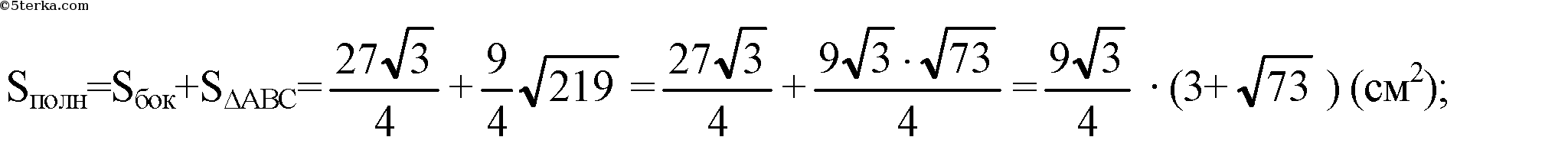
б) Построим ОК ⊥ AD, отрезок РК. По теореме о трех перпендикулярах РК⊥AD.
В квадрате диагональ ВD=2R, R — радиус описанной окружности около квадрата, ВD=2 • 3. Примем сторона квадрата равна а см, следовательно
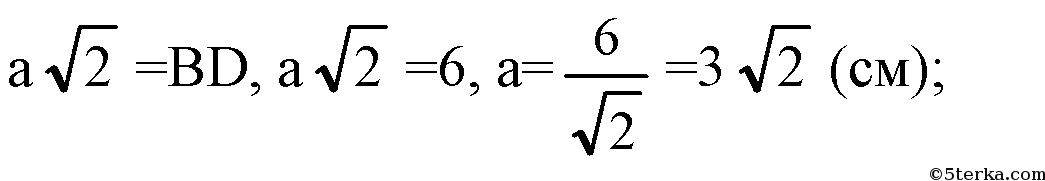
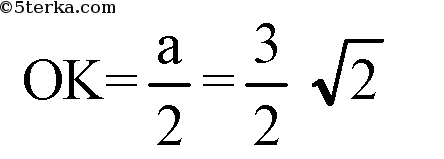
Из прямоугольного ДРОК:
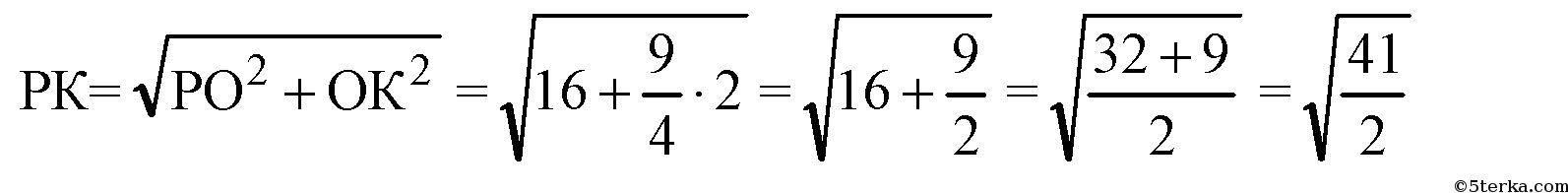
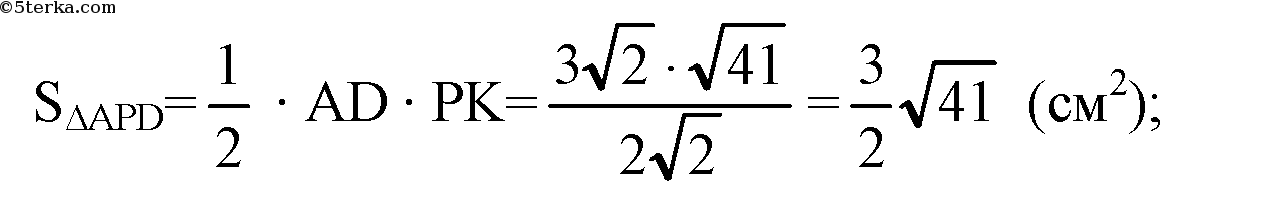
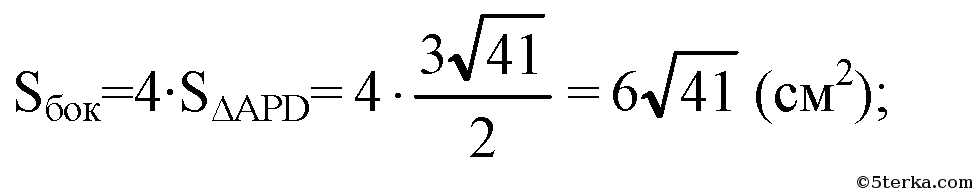
(боковые грани являются равнобедренными треугольниками);
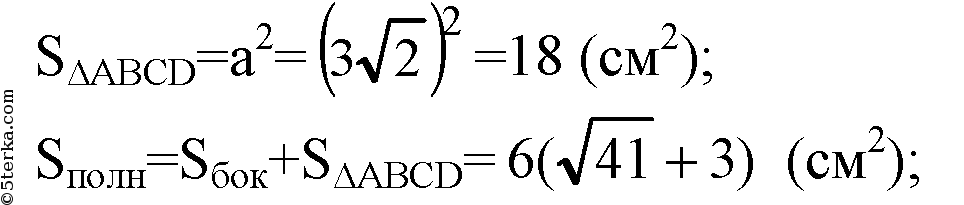
в) РО — высота конуса. Построим
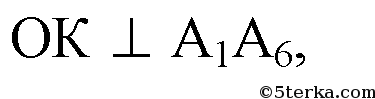
отрезок РК. По теореме о трех перпендикулярах
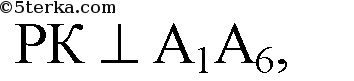

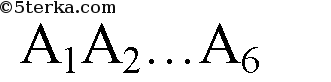
— правильный 6 — угольник. Сторона правильного 6-тиугольника равна радиусу описанной окружности.
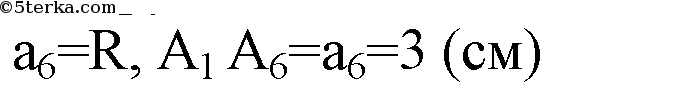
ОК — радиус вписанной в правильный 6-угольник окружности.
По теореме из планиметрии,
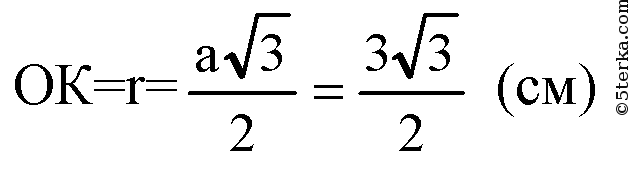
Из прямоугольного ДРОК:
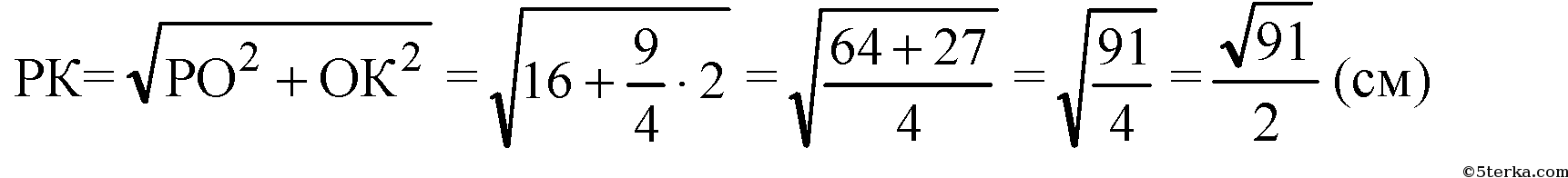
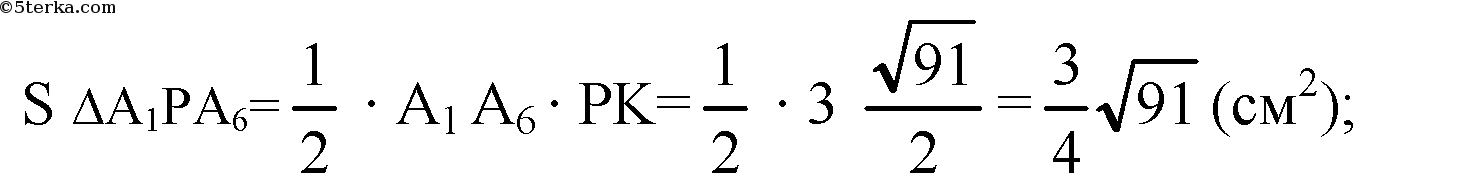
Все боковые грани — равные равнобедренные треугольники, поэтому

A1ОА6 — равносторонний, поэтому
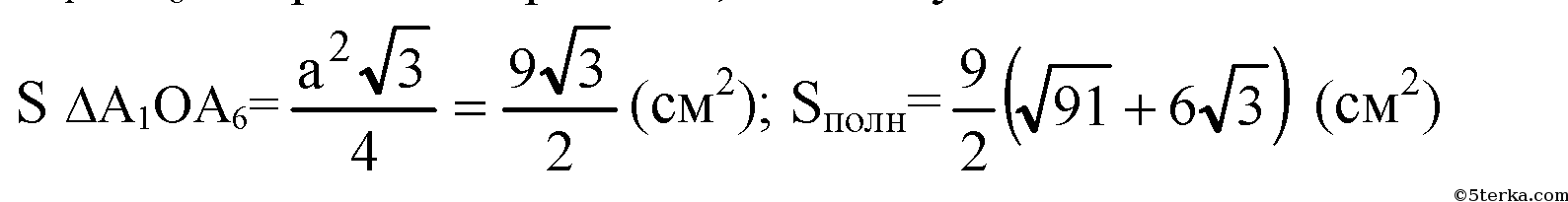
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №617
к главе «Глава VI. Цилиндр, конус и шар. Дополнительные задачи».