603. Докажите, что если плоскость параллельна оси цилиндра и расстояние между этой плоскостью и осью равно радиусу цилиндра, то плоскость содержит образующую цилиндра, и притом только одну. (В этом случае плоскость называется касательной плоскостью к цили

603. Докажите, что если плоскость параллельна оси цилиндра и расстояние между этой плоскостью и осью равно радиусу цилиндра, то плоскость содержит образующую цилиндра, и притом только одну. (В этом случае плоскость называется касательной плоскостью к цилиндру.)

Возьмем систему координат, как показано на рисунке.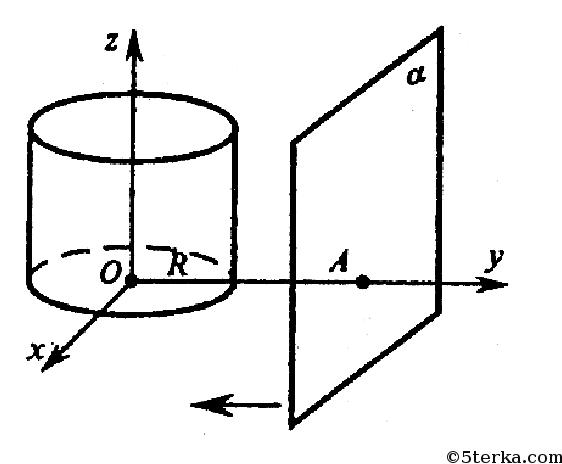

Ось ординат при этом перпендикулярна плоскости а, по оси аппликат направлена ось цилиндра. Будем приближать плоскость α к оси О_z параллельно плоскости O_xz.

Когда расстояние станет равно R, то допустим, что через точку А можно провести две прямые, параллельные оси O_z (или, что то же самое, перпендикулярные плоскости O_xy). Но по теореме п. 4 через точку А может проходить только одна прямая, параллельная оси цилиндра. Следовательно, на поверхности цилиндра найдется только одна прямая, лежащая в плоскости α и параллельная оси цилиндра, она и есть образующая цилиндра.