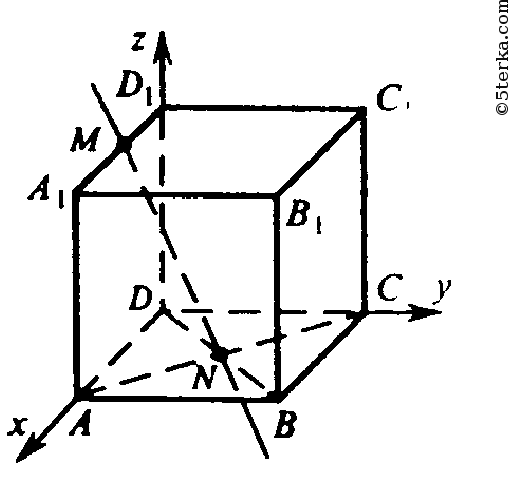
469. В кубе ABCDA1B1C1D1 диагонали грани ABCD пересекаются в точке N, а точка М лежит на ребре A1D1, причем A1M:MD1 = 1:4. Вычислите синус угла между прямой MN и плоскостью грани: a) ABCD; б) DD1C1C; в) AA1D1D.
Обозначим стороны через а.Введем прямоугольную систему координат, как
показано на рисунке. Тогда
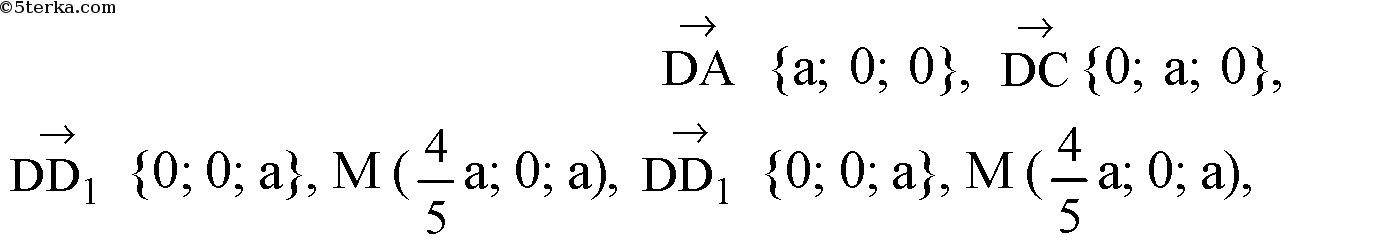
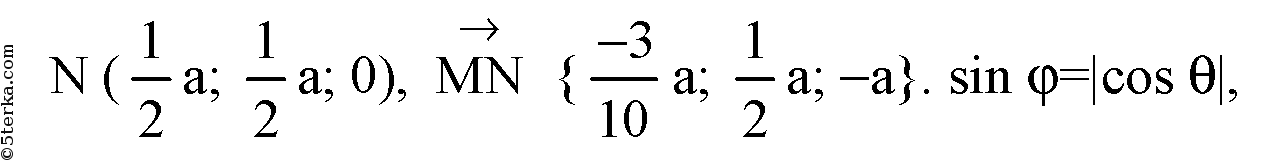
где φ — угол между прямой и плоскостью; Θ — угол между прямой и ненулевым вектором, перпендикулярным плоскости.
a) DD1 ⊥ плоскости ABCD,
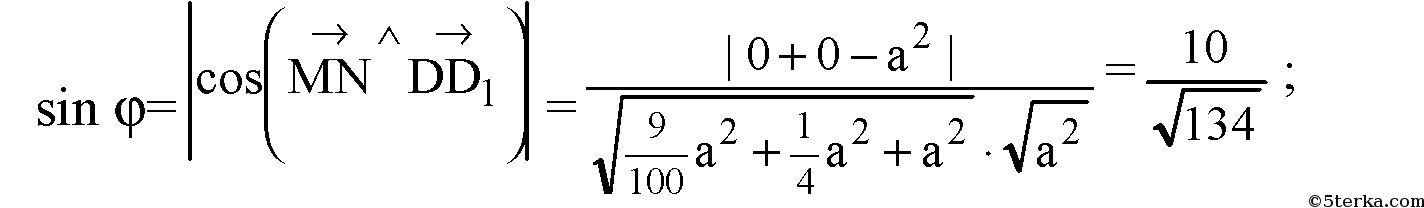
6) DA ⊥ плоскости DD1C1C,
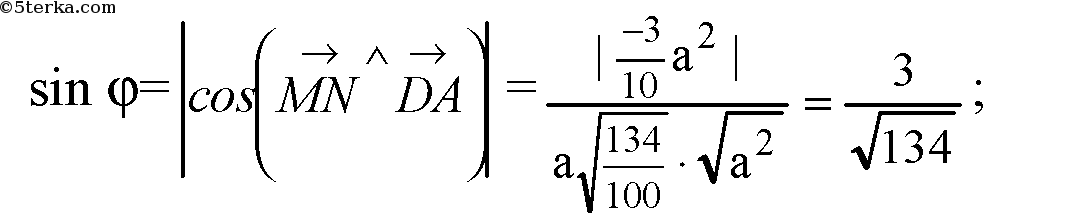
в) DC ⊥ плоскости AA1D1D,
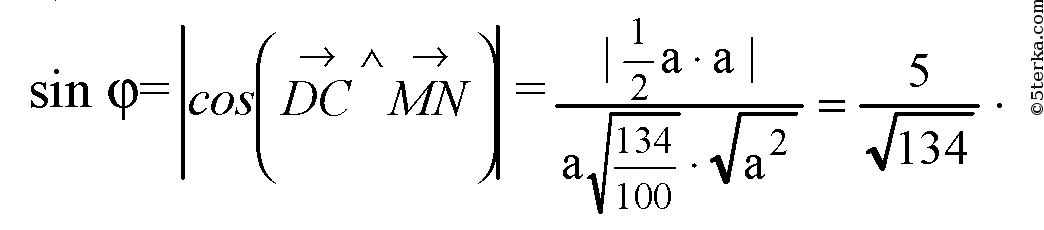
Источник:
 Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №469
к главе «Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов».
Комментарии