Р е ш е н и е. г) Векторы d{ 1; — 1; 2} и e {—2; 0; 1} не коллинеарны, так как координаты одного не пропорциональны координатам другого. Если вектор f{5; — 1; 0} можно разложить по векторам d и e, то векторы d, е и fкомпланарны. Если же вектор f нельзя разложить по векторам d и e, то векторы d, е и f не компланарны (в противном случае вектор f можно было бы разложить по векторам d и e). Таким образом, для решения задачи нужно установить, можно ли вектор f разложить по векторам d и e, т. е. существуют ли числа x и y такие, что
f=xd+ye.
Записывая это равенство в координатах, получим
Если эта система уравнений имеет решение относительно х и у, то вектор f можно разложить по векторам d и e, а если не имеет решения, то вектор f нельзя разложить по векторам d и e. В данном случае система имеет решение: х = 1, у = — 2.
Поэтому вектор f можно разложить по векторам d и e, и,
значит, векторы d, e и f компланарны.
а) Векторы
являются компланарными, т. к., записав равенство
через координаты, получим
Вектор a можно разложить по векторам
Значит векторы a , i и j компланарны.
б) Запишем равенство
через координаты:
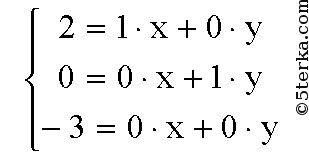
Система не имеет решений, следовательно, b , i и j не компланарны.
в) Запишем равенство
через координаты:
Значит, векторы
компланарны.
г) Векторы
не коллинеарны, т.к. координаты век
тора d не пропорциональны координатам вектора e. Если вектор
можно разложить по векторам d и e , то это значит, что векторы d , e и f компланарны. В противном случае векторы d , e и f не компланарны.
Запишем
в координатах, получим
Система имеет решение: х=1, у=-2. Поэтому вектор f можно разложить по векторам d и e , и, следовательно, векторы d , e и f компланарны.
д) Запишем равенство
в координатах:
Система не имеет решений. Поэтому векторы m , n и p не компланарны.
е) Запишем равенство
в координатах:
Система не имеет решений. Поэтому векторы
не компланарны.
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №415
к главе «Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора.».